Surjective partial differential operators on real analytic functions defined on a halfspace
Abstract
Let 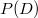 be a partial differential operator with constant coefficients and let
be a partial differential operator with constant coefficients and let 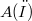 denote the real analytic functions defined on an open set
denote the real analytic functions defined on an open set 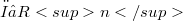 . Let H be an open halfspace. We show that
. Let H be an open halfspace. We show that 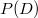 is surjective on
is surjective on 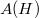 if and only if
if and only if 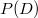 is surjective on
is surjective on 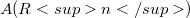 and
and 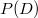 has a hyperfunction elementary solution which is real analytic on H.
has a hyperfunction elementary solution which is real analytic on H.
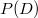 be a partial differential operator with constant coefficients and let
be a partial differential operator with constant coefficients and let 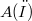 denote the real analytic functions defined on an open set
denote the real analytic functions defined on an open set 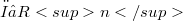 . Let H be an open halfspace. We show that
. Let H be an open halfspace. We show that 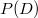 is surjective on
is surjective on 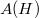 if and only if
if and only if 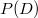 is surjective on
is surjective on 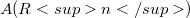 and
and 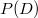 has a hyperfunction elementary solution which is real analytic on H.
has a hyperfunction elementary solution which is real analytic on H.DOI Code:
10.1285/i15900932v25n2p39
Keywords:
Partial differential equations; Elementary solutions; Surjectivity on real analytic functions
Classification:
35E20; 35E05; 35A20; 46F15
Full Text: PDF


