Introduzione
Abstract
En
We study a semi-linear initial-value problem arising from a Boltzmam like model of vahicular traffic an a motor way supposed infinite and without entrances and exits.We prove the existence and uniqueness of the local (in Time) "mild" solution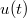
in 
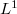and its positivity, if the initial condition 
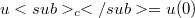is positive and belougs to 
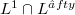. Finally,we consider the "mollified" version of the problem,already in another paper,and we show that unique strit solution 
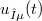is such that 
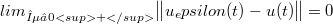uniformly in ![t ∈ [0, \buildrel \_ \over t]](http://siba-ese.unile.it/plugins/generic/latexRender/cache/efd068d36d8a5198fd04bb2af32d86c5.png)
with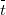 
suitably chosen.
We study a semi-linear initial-value problem arising from a Boltzmam like model of vahicular traffic an a motor way supposed infinite and without entrances and exits.We prove the existence and uniqueness of the local (in Time) "mild" solution
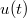in 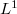and its positivity, if the initial condition 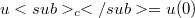is positive and belougs to 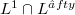. Finally,we consider the "mollified" version of the problem,already in another paper,and we show that unique strit solution 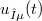is such that 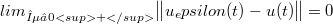uniformly in with 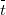suitably chosen.DOI Code:
§
Full Text: PDF
