Introduction
Abstract
En
A characterization of v-irreducible elements and of strongly v-irriducible elements of a distributive lattice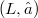 was given by D.Drake and W.J.Thorn in (1).Among other things in (1)it was proven that an element
was given by D.Drake and W.J.Thorn in (1).Among other things in (1)it was proven that an element 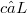 is v-irreducible if one can identify
is v-irreducible if one can identify 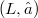 , by means of a lattice isomorphism f, with a sublattice
, by means of a lattice isomorphism f, with a sublattice 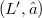 of the power set
of the power set 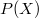 of a suitable set X, in such a way that
of a suitable set X, in such a way that 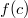 is the closure in
is the closure in 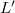 of an element
of an element 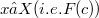 is the minimum element in
is the minimum element in 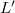 ,with respect to the set inclusion, including x).
As is well-known an element of a distributive lattice is v-irreducible iff it is v-prime.This property is exploited is an essential manner in (1).Now then in our paper we took this property as a starting point for a characterization cf v-prime and of strongly v-prime elements of any partially ordered set (in particular of any lattice).Here,on the analogy of some characterization of v-prime elements and of strongly v-prime elements of a lattice, an element c of a partially ordered set(shortly "poset"
,with respect to the set inclusion, including x).
As is well-known an element of a distributive lattice is v-irreducible iff it is v-prime.This property is exploited is an essential manner in (1).Now then in our paper we took this property as a starting point for a characterization cf v-prime and of strongly v-prime elements of any partially ordered set (in particular of any lattice).Here,on the analogy of some characterization of v-prime elements and of strongly v-prime elements of a lattice, an element c of a partially ordered set(shortly "poset" 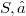 ) is said v-prime if the subset
) is said v-prime if the subset 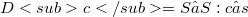 is v-directed, i.e.
is v-directed, i.e. 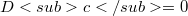 or for every
or for every 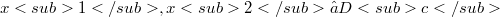 (for every(Error rendering LaTeX formula))there exists
(for every(Error rendering LaTeX formula))there exists 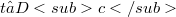 such that
such that 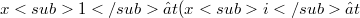 for every
for every 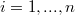 ); moreover c is said strongly v-prime if
); moreover c is said strongly v-prime if 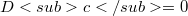 or
or 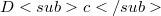 has maxium element.Then we prove than an element
has maxium element.Then we prove than an element 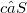 is v-prime in
is v-prime in 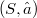 if we can identify
if we can identify 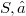 by means of an order isomorphism f,with a set (but not necessarily a lattice) of sets of the type of (1) in such a way that
by means of an order isomorphism f,with a set (but not necessarily a lattice) of sets of the type of (1) in such a way that 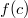 is the closure in
is the closure in 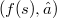 of a element of
of a element of 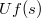 ;moreover we prove that c is strongly v-prime in
;moreover we prove that c is strongly v-prime in 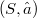 if for all function f of the above type the set
if for all function f of the above type the set 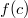 is the closure in
is the closure in 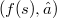 of an element of
of an element of 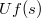 .
.
It
D.Drake e W.J.Thorn hanno in (1)una caratterizzazione degli elementi v-irriducibili e degli elementi fortemente v-irriducubili di un reticolo distributivo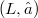 .tra l'altro in (1)è stato provato che un elemento
.tra l'altro in (1)è stato provato che un elemento 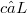 è irriducibile se e solo se si può identificare
è irriducibile se e solo se si può identificare 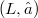 ,tramite un isomorfismo reticolare f,con un sottoreticolo
,tramite un isomorfismo reticolare f,con un sottoreticolo 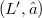 del reticolo delle parti
del reticolo delle parti 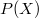 di un opportuno insieme X in tal modo che
di un opportuno insieme X in tal modo che 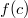 è la chiusura di
è la chiusura di 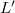 di un certo elemento
di un certo elemento 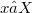 (cioè
(cioè 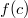 è il più piccolo elemento di
è il più piccolo elemento di 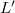 ,rispetto all'inclusione insiemistica, cui appartiene x).Come è ben noto un elemento di un reticolo distributivo è v-irriducibile se e solo se esso è v-primo.Questa propietà è usata in maniera essenziale in (1).In questo lavoro noi prendiamo lo spunto da questa propietà per dare una caratterizzazione degli elementi v-primi e degli elementi fortemente v-primi di un qualsiasi insieme parzialmente ordinato(in particolare di qualsiasi reticolo
,rispetto all'inclusione insiemistica, cui appartiene x).Come è ben noto un elemento di un reticolo distributivo è v-irriducibile se e solo se esso è v-primo.Questa propietà è usata in maniera essenziale in (1).In questo lavoro noi prendiamo lo spunto da questa propietà per dare una caratterizzazione degli elementi v-primi e degli elementi fortemente v-primi di un qualsiasi insieme parzialmente ordinato(in particolare di qualsiasi reticolo 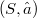 ). Precisiamo che quì, in analogia con una caratterizzazione degli elementi v-primi e degli elementi fortemente v-primi di un reticolo,un elemto c di un insieme parzialmente ordinato (
). Precisiamo che quì, in analogia con una caratterizzazione degli elementi v-primi e degli elementi fortemente v-primi di un reticolo,un elemto c di un insieme parzialmente ordinato (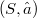 è detto v-primo se il sottoinsieme
è detto v-primo se il sottoinsieme 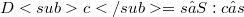 è v-diretto, cioè
è v-diretto, cioè 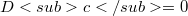 oppure per ogni
oppure per ogni 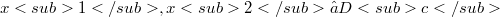 per ogni(Error rendering LaTeX formula))esiste
per ogni(Error rendering LaTeX formula))esiste 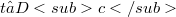 tale che
tale che 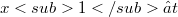 e
e 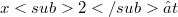 (
(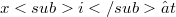 per ogni
per ogni 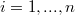 );inoltre c è detto fortemente v-primo se
);inoltre c è detto fortemente v-primo se 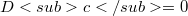 oppure
oppure 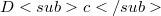 è dotato di massimo.Allora noi proviamo che un elemento
è dotato di massimo.Allora noi proviamo che un elemento 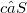 è v-primo in
è v-primo in 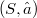 se e solo se possiamo identificare
se e solo se possiamo identificare 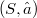 , tramite un isomorfismo f rispetto all'ordinamento, con un insieme di insiemi(non necessariamente un reticolo di insiemi) del tipo (1) in modo tale che
, tramite un isomorfismo f rispetto all'ordinamento, con un insieme di insiemi(non necessariamente un reticolo di insiemi) del tipo (1) in modo tale che 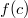 è la chiusura in (
è la chiusura in (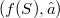 di un elemento di
di un elemento di 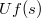 );inoltre proviamo che c è fortemente v-primo in
);inoltre proviamo che c è fortemente v-primo in 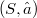 se e solo se per ogni isomorfismo f del tipo su menzionato l'insieme
se e solo se per ogni isomorfismo f del tipo su menzionato l'insieme 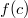 è la chiusura in
è la chiusura in 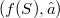 di un punto di
di un punto di 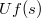 .
.
A characterization of v-irreducible elements and of strongly v-irriducible elements of a distributive lattice
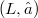 was given by D.Drake and W.J.Thorn in (1).Among other things in (1)it was proven that an element
was given by D.Drake and W.J.Thorn in (1).Among other things in (1)it was proven that an element 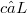 is v-irreducible if one can identify
is v-irreducible if one can identify 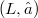 , by means of a lattice isomorphism f, with a sublattice
, by means of a lattice isomorphism f, with a sublattice 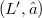 of the power set
of the power set 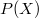 of a suitable set X, in such a way that
of a suitable set X, in such a way that 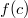 is the closure in
is the closure in 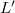 of an element
of an element 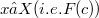 is the minimum element in
is the minimum element in 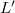 ,with respect to the set inclusion, including x).
As is well-known an element of a distributive lattice is v-irreducible iff it is v-prime.This property is exploited is an essential manner in (1).Now then in our paper we took this property as a starting point for a characterization cf v-prime and of strongly v-prime elements of any partially ordered set (in particular of any lattice).Here,on the analogy of some characterization of v-prime elements and of strongly v-prime elements of a lattice, an element c of a partially ordered set(shortly "poset"
,with respect to the set inclusion, including x).
As is well-known an element of a distributive lattice is v-irreducible iff it is v-prime.This property is exploited is an essential manner in (1).Now then in our paper we took this property as a starting point for a characterization cf v-prime and of strongly v-prime elements of any partially ordered set (in particular of any lattice).Here,on the analogy of some characterization of v-prime elements and of strongly v-prime elements of a lattice, an element c of a partially ordered set(shortly "poset" 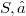 ) is said v-prime if the subset
) is said v-prime if the subset 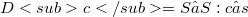 is v-directed, i.e.
is v-directed, i.e. 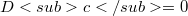 or for every
or for every 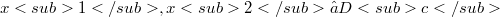 (for every(Error rendering LaTeX formula))there exists
(for every(Error rendering LaTeX formula))there exists 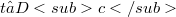 such that
such that 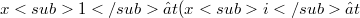 for every
for every 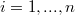 ); moreover c is said strongly v-prime if
); moreover c is said strongly v-prime if 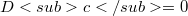 or
or 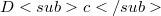 has maxium element.Then we prove than an element
has maxium element.Then we prove than an element 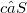 is v-prime in
is v-prime in 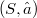 if we can identify
if we can identify 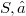 by means of an order isomorphism f,with a set (but not necessarily a lattice) of sets of the type of (1) in such a way that
by means of an order isomorphism f,with a set (but not necessarily a lattice) of sets of the type of (1) in such a way that 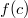 is the closure in
is the closure in 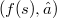 of a element of
of a element of 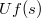 ;moreover we prove that c is strongly v-prime in
;moreover we prove that c is strongly v-prime in 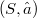 if for all function f of the above type the set
if for all function f of the above type the set 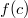 is the closure in
is the closure in 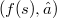 of an element of
of an element of 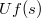 .
.It
D.Drake e W.J.Thorn hanno in (1)una caratterizzazione degli elementi v-irriducibili e degli elementi fortemente v-irriducubili di un reticolo distributivo
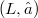 .tra l'altro in (1)è stato provato che un elemento
.tra l'altro in (1)è stato provato che un elemento 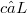 è irriducibile se e solo se si può identificare
è irriducibile se e solo se si può identificare 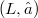 ,tramite un isomorfismo reticolare f,con un sottoreticolo
,tramite un isomorfismo reticolare f,con un sottoreticolo 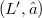 del reticolo delle parti
del reticolo delle parti 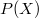 di un opportuno insieme X in tal modo che
di un opportuno insieme X in tal modo che 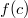 è la chiusura di
è la chiusura di 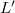 di un certo elemento
di un certo elemento 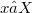 (cioè
(cioè 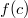 è il più piccolo elemento di
è il più piccolo elemento di 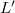 ,rispetto all'inclusione insiemistica, cui appartiene x).Come è ben noto un elemento di un reticolo distributivo è v-irriducibile se e solo se esso è v-primo.Questa propietà è usata in maniera essenziale in (1).In questo lavoro noi prendiamo lo spunto da questa propietà per dare una caratterizzazione degli elementi v-primi e degli elementi fortemente v-primi di un qualsiasi insieme parzialmente ordinato(in particolare di qualsiasi reticolo
,rispetto all'inclusione insiemistica, cui appartiene x).Come è ben noto un elemento di un reticolo distributivo è v-irriducibile se e solo se esso è v-primo.Questa propietà è usata in maniera essenziale in (1).In questo lavoro noi prendiamo lo spunto da questa propietà per dare una caratterizzazione degli elementi v-primi e degli elementi fortemente v-primi di un qualsiasi insieme parzialmente ordinato(in particolare di qualsiasi reticolo 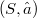 ). Precisiamo che quì, in analogia con una caratterizzazione degli elementi v-primi e degli elementi fortemente v-primi di un reticolo,un elemto c di un insieme parzialmente ordinato (
). Precisiamo che quì, in analogia con una caratterizzazione degli elementi v-primi e degli elementi fortemente v-primi di un reticolo,un elemto c di un insieme parzialmente ordinato (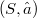 è detto v-primo se il sottoinsieme
è detto v-primo se il sottoinsieme 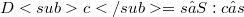 è v-diretto, cioè
è v-diretto, cioè 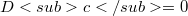 oppure per ogni
oppure per ogni 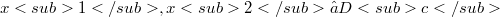 per ogni(Error rendering LaTeX formula))esiste
per ogni(Error rendering LaTeX formula))esiste 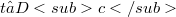 tale che
tale che 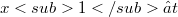 e
e 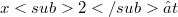 (
(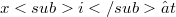 per ogni
per ogni 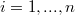 );inoltre c è detto fortemente v-primo se
);inoltre c è detto fortemente v-primo se 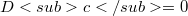 oppure
oppure 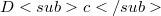 è dotato di massimo.Allora noi proviamo che un elemento
è dotato di massimo.Allora noi proviamo che un elemento 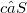 è v-primo in
è v-primo in 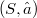 se e solo se possiamo identificare
se e solo se possiamo identificare 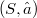 , tramite un isomorfismo f rispetto all'ordinamento, con un insieme di insiemi(non necessariamente un reticolo di insiemi) del tipo (1) in modo tale che
, tramite un isomorfismo f rispetto all'ordinamento, con un insieme di insiemi(non necessariamente un reticolo di insiemi) del tipo (1) in modo tale che 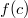 è la chiusura in (
è la chiusura in (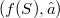 di un elemento di
di un elemento di 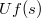 );inoltre proviamo che c è fortemente v-primo in
);inoltre proviamo che c è fortemente v-primo in 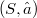 se e solo se per ogni isomorfismo f del tipo su menzionato l'insieme
se e solo se per ogni isomorfismo f del tipo su menzionato l'insieme 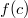 è la chiusura in
è la chiusura in 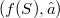 di un punto di
di un punto di 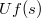 .
.DOI Code:
§
Full Text: PDF


