Introduzione
Abstract
En
In the present note we study the integro-differenzial equation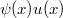
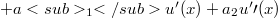
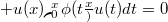 for wich we obtain theorems on existence, uniqueness and continuous dependence on data. The case
for wich we obtain theorems on existence, uniqueness and continuous dependence on data. The case 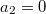 , has been investigated by M.A. Sneider in "Saggio di una teoria per un'equazione integro-differenziale che interessa la dinamica delle galassie",Rendiconti di Matematica (4)vol6 serieVI (1973). The methods used can also be applied to the case of integro-differential equations analogous to the previous one but in wich the differential part is of the from(Error rendering LaTeX formula) with
, has been investigated by M.A. Sneider in "Saggio di una teoria per un'equazione integro-differenziale che interessa la dinamica delle galassie",Rendiconti di Matematica (4)vol6 serieVI (1973). The methods used can also be applied to the case of integro-differential equations analogous to the previous one but in wich the differential part is of the from(Error rendering LaTeX formula) with 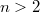 .
.
It
In questo lavoro si studia l'equazione integro-differenziale(Error rendering LaTeX formula) nella funzione incognita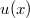 , e si ottengono teoremi di esistenza, unicità dipendenza continua dai dati. Il caso
, e si ottengono teoremi di esistenza, unicità dipendenza continua dai dati. Il caso 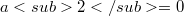 , è stato studiato da M.A. Sneider, in ""Saggio di una teoria per un'equazione integro-differenziale che interessa la dinamica delle galassie",Rendiconti di Matematica (4)vol6 serieVI (1973).I metodi adoperati sono ugualmente applicabili al caso di equazione integro-differenziale analoghe alla precedente in cui la parte differenziale è della forma(Error rendering LaTeX formula) con
, è stato studiato da M.A. Sneider, in ""Saggio di una teoria per un'equazione integro-differenziale che interessa la dinamica delle galassie",Rendiconti di Matematica (4)vol6 serieVI (1973).I metodi adoperati sono ugualmente applicabili al caso di equazione integro-differenziale analoghe alla precedente in cui la parte differenziale è della forma(Error rendering LaTeX formula) con 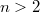
In the present note we study the integro-differenzial equation
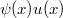
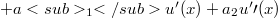
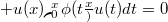 for wich we obtain theorems on existence, uniqueness and continuous dependence on data. The case
for wich we obtain theorems on existence, uniqueness and continuous dependence on data. The case 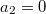 , has been investigated by M.A. Sneider in "Saggio di una teoria per un'equazione integro-differenziale che interessa la dinamica delle galassie",Rendiconti di Matematica (4)vol6 serieVI (1973). The methods used can also be applied to the case of integro-differential equations analogous to the previous one but in wich the differential part is of the from(Error rendering LaTeX formula) with
, has been investigated by M.A. Sneider in "Saggio di una teoria per un'equazione integro-differenziale che interessa la dinamica delle galassie",Rendiconti di Matematica (4)vol6 serieVI (1973). The methods used can also be applied to the case of integro-differential equations analogous to the previous one but in wich the differential part is of the from(Error rendering LaTeX formula) with 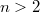 .
.It
In questo lavoro si studia l'equazione integro-differenziale(Error rendering LaTeX formula) nella funzione incognita
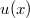 , e si ottengono teoremi di esistenza, unicità dipendenza continua dai dati. Il caso
, e si ottengono teoremi di esistenza, unicità dipendenza continua dai dati. Il caso 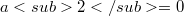 , è stato studiato da M.A. Sneider, in ""Saggio di una teoria per un'equazione integro-differenziale che interessa la dinamica delle galassie",Rendiconti di Matematica (4)vol6 serieVI (1973).I metodi adoperati sono ugualmente applicabili al caso di equazione integro-differenziale analoghe alla precedente in cui la parte differenziale è della forma(Error rendering LaTeX formula) con
, è stato studiato da M.A. Sneider, in ""Saggio di una teoria per un'equazione integro-differenziale che interessa la dinamica delle galassie",Rendiconti di Matematica (4)vol6 serieVI (1973).I metodi adoperati sono ugualmente applicabili al caso di equazione integro-differenziale analoghe alla precedente in cui la parte differenziale è della forma(Error rendering LaTeX formula) con 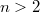
DOI Code:
§
Full Text: PDF


