Introduzione
Abstract
It
Dati uno spazio topologico normale e numerabilmente paracompatto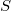 ed un grafo finito ed orientato
ed un grafo finito ed orientato 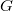 si prova che tra gli insiemi
si prova che tra gli insiemi 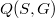 e
e 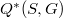 delle classi di o-omotopia e di o*-omotopia esiste una biiezione naturale.Nelle stesse condizioni, se
delle classi di o-omotopia e di o*-omotopia esiste una biiezione naturale.Nelle stesse condizioni, se 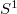 è un sottospazio chiuso di
è un sottospazio chiuso di 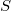 e
e 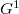 un sottografo di
un sottografo di 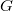 , esiste ancora una biiezione naturale tra gli insiemi
, esiste ancora una biiezione naturale tra gli insiemi 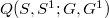 e
e 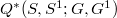 delle classi di omotopia.Si mostra infine che in condizioni meno restrittive per lo spazio S le precedenti biiezioni possono non sussistere.
delle classi di omotopia.Si mostra infine che in condizioni meno restrittive per lo spazio S le precedenti biiezioni possono non sussistere.
Dati uno spazio topologico normale e numerabilmente paracompatto
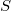 ed un grafo finito ed orientato
ed un grafo finito ed orientato 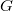 si prova che tra gli insiemi
si prova che tra gli insiemi 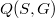 e
e 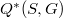 delle classi di o-omotopia e di o*-omotopia esiste una biiezione naturale.Nelle stesse condizioni, se
delle classi di o-omotopia e di o*-omotopia esiste una biiezione naturale.Nelle stesse condizioni, se 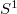 è un sottospazio chiuso di
è un sottospazio chiuso di 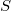 e
e 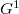 un sottografo di
un sottografo di 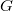 , esiste ancora una biiezione naturale tra gli insiemi
, esiste ancora una biiezione naturale tra gli insiemi 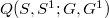 e
e 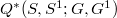 delle classi di omotopia.Si mostra infine che in condizioni meno restrittive per lo spazio S le precedenti biiezioni possono non sussistere.
delle classi di omotopia.Si mostra infine che in condizioni meno restrittive per lo spazio S le precedenti biiezioni possono non sussistere.DOI Code:
§
Full Text: PDF


