Introduzione
Abstract
En
Given a topological space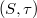 and a subset
and a subset 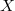 of
of 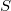 , the topology
, the topology 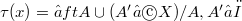 is called the simple extension of
is called the simple extension of  by
by 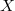 (see Levine 3).Here we show how to recognize when two subsets
(see Levine 3).Here we show how to recognize when two subsets 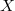 and
and 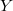 of
of 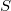 define the same simple extension of
define the same simple extension of  and we give a characterization of those expansions of
and we give a characterization of those expansions of  which are simple extensions of
which are simple extensions of  by suitable subsets of
by suitable subsets of 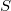 .
.
Given a topological space
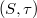 and a subset
and a subset 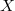 of
of 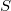 , the topology
, the topology 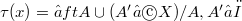 is called the simple extension of
is called the simple extension of  by
by 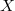 (see Levine 3).Here we show how to recognize when two subsets
(see Levine 3).Here we show how to recognize when two subsets 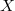 and
and 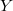 of
of 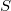 define the same simple extension of
define the same simple extension of  and we give a characterization of those expansions of
and we give a characterization of those expansions of  which are simple extensions of
which are simple extensions of  by suitable subsets of
by suitable subsets of 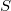 .
.DOI Code:
§
Full Text: PDF


