Introduzione
Abstract
En
In this note we observe a decreasing property of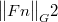 along the numerical solution of the autonomous differential system
along the numerical solution of the autonomous differential system 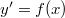 which satisfies a monotonicity condition;such a solution is obtained by means of a class of linear k-step A-stable methods and we have set(Error rendering LaTeX formula) and G is a symmetric positive definite matrix of order k. We study also a particular subclass of linear multistep G-stable methods of maximum order,in which the matrix G is actually constructed.The associated Lyapunov function ensures the stability of the set of equilibrium points.
which satisfies a monotonicity condition;such a solution is obtained by means of a class of linear k-step A-stable methods and we have set(Error rendering LaTeX formula) and G is a symmetric positive definite matrix of order k. We study also a particular subclass of linear multistep G-stable methods of maximum order,in which the matrix G is actually constructed.The associated Lyapunov function ensures the stability of the set of equilibrium points.
In this note we observe a decreasing property of
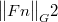 along the numerical solution of the autonomous differential system
along the numerical solution of the autonomous differential system 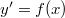 which satisfies a monotonicity condition;such a solution is obtained by means of a class of linear k-step A-stable methods and we have set(Error rendering LaTeX formula) and G is a symmetric positive definite matrix of order k. We study also a particular subclass of linear multistep G-stable methods of maximum order,in which the matrix G is actually constructed.The associated Lyapunov function ensures the stability of the set of equilibrium points.
which satisfies a monotonicity condition;such a solution is obtained by means of a class of linear k-step A-stable methods and we have set(Error rendering LaTeX formula) and G is a symmetric positive definite matrix of order k. We study also a particular subclass of linear multistep G-stable methods of maximum order,in which the matrix G is actually constructed.The associated Lyapunov function ensures the stability of the set of equilibrium points.DOI Code:
§
Full Text: PDF


