Introduzione
Abstract
En
On concluding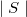 , J. Sezp suggested the study of a spacial algebra
, J. Sezp suggested the study of a spacial algebra 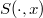 ,where "
,where " " is a group operation (instead of
" is a group operation (instead of 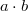 we shall write ab) and "x" is a semigroup operation with an idempotent element e; moreover
we shall write ab) and "x" is a semigroup operation with an idempotent element e; moreover 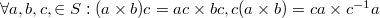 where
where 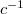 is the inverse of c in
is the inverse of c in 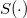 . The aim of this work is to analyze such an algebra.
. The aim of this work is to analyze such an algebra.
On concluding
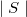 , J. Sezp suggested the study of a spacial algebra
, J. Sezp suggested the study of a spacial algebra 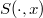 ,where "
,where " " is a group operation (instead of
" is a group operation (instead of 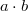 we shall write ab) and "x" is a semigroup operation with an idempotent element e; moreover
we shall write ab) and "x" is a semigroup operation with an idempotent element e; moreover 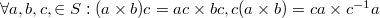 where
where 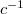 is the inverse of c in
is the inverse of c in 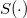 . The aim of this work is to analyze such an algebra.
. The aim of this work is to analyze such an algebra.DOI Code:
§
Full Text: PDF


