Introduzione
Abstract
En
Given a set
, a finitely additive probability measure 
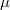on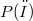 
is considered. Let 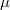be "strongly" non-atomic: we prove that there exists a sequence 
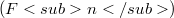of subsets of (mutually disjoint and with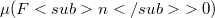 
) whose union has measure equal to an arbitrarily given 𝛼 (with 
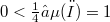) and such that 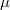is countably additive on them. As a simple corollary, the following property (well-known for countably additive measures)is deduced: the range of 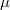is the whole interval [0,1]. In the last part of the paper, some aspects of a decomposition theorem by B. De Finetti (for an arbitrary 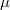) are deepened.
Given a set
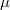, a finitely additive probability measure on 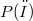is considered. Let 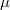be "strongly" non-atomic: we prove that there exists a sequence 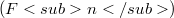of subsets of (mutually disjoint and with 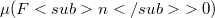) whose union has measure equal to an arbitrarily given 𝛼 (with 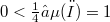) and such that 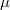is countably additive on them. As a simple corollary, the following property (well-known for countably additive measures)is deduced: the range of 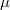is the whole interval [0,1]. In the last part of the paper, some aspects of a decomposition theorem by B. De Finetti (for an arbitrary 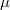) are deepened.DOI Code:
Full Text: PDF
