On vector-valued sequence spaces
Abstract
In this paper we investigate the topological properties of vector valued sequence spaces. After an introduction of normal Banach sequence spaces λ we consider the vector valued sequence spaces 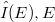 a locally convex Hausdorff space and we prove some basic facts concerning this spaces.We give complete characterizations for barrelled vector valued
a locally convex Hausdorff space and we prove some basic facts concerning this spaces.We give complete characterizations for barrelled vector valued  spaces and distinguished vector valued Fréchet spaces. At the end we give sufficient conditions guaranteeing that
spaces and distinguished vector valued Fréchet spaces. At the end we give sufficient conditions guaranteeing that 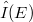 is bornological.
is bornological.
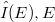 a locally convex Hausdorff space and we prove some basic facts concerning this spaces.We give complete characterizations for barrelled vector valued
a locally convex Hausdorff space and we prove some basic facts concerning this spaces.We give complete characterizations for barrelled vector valued 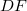 spaces and distinguished vector valued Fréchet spaces. At the end we give sufficient conditions guaranteeing that
spaces and distinguished vector valued Fréchet spaces. At the end we give sufficient conditions guaranteeing that 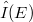 is bornological.
is bornological.DOI Code:
10.1285/i15900932v14n1p1
Full Text: PDF


