On the class of contact metric manifolds with a 3-τ-structure
Abstract
In [7] Gouli-Andreou and Xenos introduced the notion of a contact metric strutture being a 3-τ-structure and developed some of its basic properties. Known examples however are contact metric manifolds satisfying the stronger condition that their Ricci operator commute with the fundamental collineation 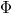 . In this paper we show that contact metric manifolds with a 3-τ-structure indeed form a larger class and the example we give is also of interest in terms of special directions introduced in [3] on contact metric manifolds with negative sectional curvature for plane sections containing the characteristic vector field
. In this paper we show that contact metric manifolds with a 3-τ-structure indeed form a larger class and the example we give is also of interest in terms of special directions introduced in [3] on contact metric manifolds with negative sectional curvature for plane sections containing the characteristic vector field 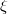 .
.
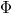 . In this paper we show that contact metric manifolds with a 3-τ-structure indeed form a larger class and the example we give is also of interest in terms of special directions introduced in [3] on contact metric manifolds with negative sectional curvature for plane sections containing the characteristic vector field
. In this paper we show that contact metric manifolds with a 3-τ-structure indeed form a larger class and the example we give is also of interest in terms of special directions introduced in [3] on contact metric manifolds with negative sectional curvature for plane sections containing the characteristic vector field 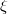 .
.DOI Code:
10.1285/i15900932v16n1p99
Full Text: PDF


