Geometric-combinatorial characteristics of cones
Abstract
It is shown for a proper closed locally compact subset S of a real normed linear space X that(Error rendering LaTeX formula), where 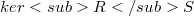 is the R-kernel of S,
is the R-kernel of S, 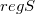 denotes the set of regular points of S and(Error rendering LaTeX formula). Furthermore, it is shown for a closed connected nonconvex subset S of X that(Error rendering LaTeX formula), where D is a relatively open subset of S containing the set
denotes the set of regular points of S and(Error rendering LaTeX formula). Furthermore, it is shown for a closed connected nonconvex subset S of X that(Error rendering LaTeX formula), where D is a relatively open subset of S containing the set 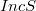 of local nonconvexity points of S. If X is a uniformly convex and uniformly smooth real Banach space, then the first of these formulae is shown to hold with the set
of local nonconvexity points of S. If X is a uniformly convex and uniformly smooth real Banach space, then the first of these formulae is shown to hold with the set 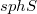 of spherical points of S in place of
of spherical points of S in place of 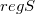 , and the second one for a closed connected nonconvex set S. For a connected subset S of a real topological linear space L with nonempty
, and the second one for a closed connected nonconvex set S. For a connected subset S of a real topological linear space L with nonempty 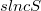 , the set of strong local nonconvexity points of S, it is shown that(Error rendering LaTeX formula), where
, the set of strong local nonconvexity points of S, it is shown that(Error rendering LaTeX formula), where 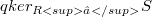 is the quasi-
is the quasi-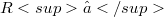 -kernel of S and(Error rendering LaTeX formula), and that the equality holds provided, in addition, S is open. In conjunction with an infinite-dimensional version of Helly's theorem for flats, these intersection formulae generate Krasnosel‘skii-type characterizations of cones and quasi-cones. All this parallels the
research done recently by the author for starshaped and quasi-starshaped sets.
-kernel of S and(Error rendering LaTeX formula), and that the equality holds provided, in addition, S is open. In conjunction with an infinite-dimensional version of Helly's theorem for flats, these intersection formulae generate Krasnosel‘skii-type characterizations of cones and quasi-cones. All this parallels the
research done recently by the author for starshaped and quasi-starshaped sets.
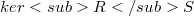 is the R-kernel of S,
is the R-kernel of S, 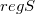 denotes the set of regular points of S and(Error rendering LaTeX formula). Furthermore, it is shown for a closed connected nonconvex subset S of X that(Error rendering LaTeX formula), where D is a relatively open subset of S containing the set
denotes the set of regular points of S and(Error rendering LaTeX formula). Furthermore, it is shown for a closed connected nonconvex subset S of X that(Error rendering LaTeX formula), where D is a relatively open subset of S containing the set 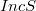 of local nonconvexity points of S. If X is a uniformly convex and uniformly smooth real Banach space, then the first of these formulae is shown to hold with the set
of local nonconvexity points of S. If X is a uniformly convex and uniformly smooth real Banach space, then the first of these formulae is shown to hold with the set 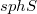 of spherical points of S in place of
of spherical points of S in place of 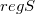 , and the second one for a closed connected nonconvex set S. For a connected subset S of a real topological linear space L with nonempty
, and the second one for a closed connected nonconvex set S. For a connected subset S of a real topological linear space L with nonempty 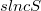 , the set of strong local nonconvexity points of S, it is shown that(Error rendering LaTeX formula), where
, the set of strong local nonconvexity points of S, it is shown that(Error rendering LaTeX formula), where 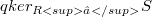 is the quasi-
is the quasi-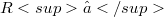 -kernel of S and(Error rendering LaTeX formula), and that the equality holds provided, in addition, S is open. In conjunction with an infinite-dimensional version of Helly's theorem for flats, these intersection formulae generate Krasnosel‘skii-type characterizations of cones and quasi-cones. All this parallels the
research done recently by the author for starshaped and quasi-starshaped sets.
-kernel of S and(Error rendering LaTeX formula), and that the equality holds provided, in addition, S is open. In conjunction with an infinite-dimensional version of Helly's theorem for flats, these intersection formulae generate Krasnosel‘skii-type characterizations of cones and quasi-cones. All this parallels the
research done recently by the author for starshaped and quasi-starshaped sets.DOI Code:
10.1285/i15900932v16n1p59
Full Text: PDF


