Weighted spaces of holomorphic functions and sequence spaces
Abstract
Our aim in this note is twofold. Firstly we show that, given any Köthe echelon space of order one, a weighted limit of Banach spaces of holomorphic functions on the disc can be constructed such that the strong dual of the sequence space is isomorphic to a complemented subspace of the projective hull associated with the weighted inductive limit. It is also proved that, under some mild assumptions, a weighted inductive limit of spaces of holomorphic functions is a 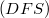 - space (and hence the projective description holds) if and only if the associated weights satisfy the condition
- space (and hence the projective description holds) if and only if the associated weights satisfy the condition 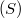 of Bierstedt, Meise and Summers.
of Bierstedt, Meise and Summers.
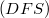 - space (and hence the projective description holds) if and only if the associated weights satisfy the condition
- space (and hence the projective description holds) if and only if the associated weights satisfy the condition 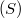 of Bierstedt, Meise and Summers.
of Bierstedt, Meise and Summers.DOI Code:
10.1285/i15900932v17p87
Keywords:
Weighted inductive limits; Spaces of holomorphic funtions; Köthe sequence spaces
Classification:
46E10; 46A13; 46A04; 46A45
Full Text: PDF


