An extension theorem for bilinear forms
Abstract
Apart from the fundamental interest in a weak characterization of quadratic forms the possibility to extend quadratic forms defined on subspaces of a vector space 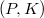 to a common form on P is helpfull in the representation of higher dimensional geometries as well as in characterizing quadrics by their plane sections. In the case that all vector subspaces endowed with a quadratic form are three-dimensional, there are extension theorems, first under additional conditions by J. Tits [1], H.-J. Kroll [4], K. J. Dienst, H. Mäurer [2], E. M. Schröder [7], H. Maürer [6] and finally in the most general form by E. M. Schröder [8], [10].
Apparently there are only two papers investigating under which conditions quadratic forms defined on two-dimensional vector subspaces posess a common extension. In [9], (8.7) E. M. Schröder showed how to extend quadratic forms defined on two-dimensional vector subspaces of a given three-dimensional vector space by employing the hexagram-condition. In [5] euclidean spaces of arbitrary dimension are described by an axiom system relating only to incidence and congruence. Taking euclidean planes for granted, it is required that every plane of the space is an euclidean plane. By a further axiom all planes are made compatible. Based on the method of [4] it is possible to construct a quadratic form which describes the congruence relation. For this construction H. Karzel gave a direct proof in [3]. Implicitly in his proof in the case of characteristic
to a common form on P is helpfull in the representation of higher dimensional geometries as well as in characterizing quadrics by their plane sections. In the case that all vector subspaces endowed with a quadratic form are three-dimensional, there are extension theorems, first under additional conditions by J. Tits [1], H.-J. Kroll [4], K. J. Dienst, H. Mäurer [2], E. M. Schröder [7], H. Maürer [6] and finally in the most general form by E. M. Schröder [8], [10].
Apparently there are only two papers investigating under which conditions quadratic forms defined on two-dimensional vector subspaces posess a common extension. In [9], (8.7) E. M. Schröder showed how to extend quadratic forms defined on two-dimensional vector subspaces of a given three-dimensional vector space by employing the hexagram-condition. In [5] euclidean spaces of arbitrary dimension are described by an axiom system relating only to incidence and congruence. Taking euclidean planes for granted, it is required that every plane of the space is an euclidean plane. By a further axiom all planes are made compatible. Based on the method of [4] it is possible to construct a quadratic form which describes the congruence relation. For this construction H. Karzel gave a direct proof in [3]. Implicitly in his proof in the case of characteristic 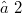 anisotropic symmetric bilinear forms are extended from two-dimensional vector subspaces to the vector space containing them.
In this paper we prove an extension theorem for symmetric bilinear forms defined on two-dimensional vector subspaces. In the case of characteristic 2 our proof is not valid for quadratic forms but only for bilinear forms with sufficiently many anisotropic vectors. On the other side in the case of a characteristic
anisotropic symmetric bilinear forms are extended from two-dimensional vector subspaces to the vector space containing them.
In this paper we prove an extension theorem for symmetric bilinear forms defined on two-dimensional vector subspaces. In the case of characteristic 2 our proof is not valid for quadratic forms but only for bilinear forms with sufficiently many anisotropic vectors. On the other side in the case of a characteristic 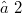 Satz (3.2) in [8] is a direct conclusion of our theorem.
Gratefully at the end of section 1 we repeat a comment of this paper's referee, that our theorem might be deduced from a general representation theorem for polarities. But in section 2 the extension will be constructed directly.
Satz (3.2) in [8] is a direct conclusion of our theorem.
Gratefully at the end of section 1 we repeat a comment of this paper's referee, that our theorem might be deduced from a general representation theorem for polarities. But in section 2 the extension will be constructed directly.
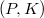 to a common form on P is helpfull in the representation of higher dimensional geometries as well as in characterizing quadrics by their plane sections. In the case that all vector subspaces endowed with a quadratic form are three-dimensional, there are extension theorems, first under additional conditions by J. Tits [1], H.-J. Kroll [4], K. J. Dienst, H. Mäurer [2], E. M. Schröder [7], H. Maürer [6] and finally in the most general form by E. M. Schröder [8], [10].
Apparently there are only two papers investigating under which conditions quadratic forms defined on two-dimensional vector subspaces posess a common extension. In [9], (8.7) E. M. Schröder showed how to extend quadratic forms defined on two-dimensional vector subspaces of a given three-dimensional vector space by employing the hexagram-condition. In [5] euclidean spaces of arbitrary dimension are described by an axiom system relating only to incidence and congruence. Taking euclidean planes for granted, it is required that every plane of the space is an euclidean plane. By a further axiom all planes are made compatible. Based on the method of [4] it is possible to construct a quadratic form which describes the congruence relation. For this construction H. Karzel gave a direct proof in [3]. Implicitly in his proof in the case of characteristic
to a common form on P is helpfull in the representation of higher dimensional geometries as well as in characterizing quadrics by their plane sections. In the case that all vector subspaces endowed with a quadratic form are three-dimensional, there are extension theorems, first under additional conditions by J. Tits [1], H.-J. Kroll [4], K. J. Dienst, H. Mäurer [2], E. M. Schröder [7], H. Maürer [6] and finally in the most general form by E. M. Schröder [8], [10].
Apparently there are only two papers investigating under which conditions quadratic forms defined on two-dimensional vector subspaces posess a common extension. In [9], (8.7) E. M. Schröder showed how to extend quadratic forms defined on two-dimensional vector subspaces of a given three-dimensional vector space by employing the hexagram-condition. In [5] euclidean spaces of arbitrary dimension are described by an axiom system relating only to incidence and congruence. Taking euclidean planes for granted, it is required that every plane of the space is an euclidean plane. By a further axiom all planes are made compatible. Based on the method of [4] it is possible to construct a quadratic form which describes the congruence relation. For this construction H. Karzel gave a direct proof in [3]. Implicitly in his proof in the case of characteristic 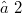 anisotropic symmetric bilinear forms are extended from two-dimensional vector subspaces to the vector space containing them.
In this paper we prove an extension theorem for symmetric bilinear forms defined on two-dimensional vector subspaces. In the case of characteristic 2 our proof is not valid for quadratic forms but only for bilinear forms with sufficiently many anisotropic vectors. On the other side in the case of a characteristic
anisotropic symmetric bilinear forms are extended from two-dimensional vector subspaces to the vector space containing them.
In this paper we prove an extension theorem for symmetric bilinear forms defined on two-dimensional vector subspaces. In the case of characteristic 2 our proof is not valid for quadratic forms but only for bilinear forms with sufficiently many anisotropic vectors. On the other side in the case of a characteristic 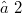 Satz (3.2) in [8] is a direct conclusion of our theorem.
Gratefully at the end of section 1 we repeat a comment of this paper's referee, that our theorem might be deduced from a general representation theorem for polarities. But in section 2 the extension will be constructed directly.
Satz (3.2) in [8] is a direct conclusion of our theorem.
Gratefully at the end of section 1 we repeat a comment of this paper's referee, that our theorem might be deduced from a general representation theorem for polarities. But in section 2 the extension will be constructed directly.DOI Code:
10.1285/i15900932v18n2p291
Full Text: PDF


