Action of classical groups on the varieties associated with skew field extensions
Abstract
Let 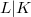 be a finite skew field extension, K commutative and V a finite dimensional vector space over L. We study the action of general L-linear groups on the set of K-subspaces of V and the action of unitary groups on the set of
be a finite skew field extension, K commutative and V a finite dimensional vector space over L. We study the action of general L-linear groups on the set of K-subspaces of V and the action of unitary groups on the set of 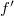 -isotropic K-subspaces of V. In the latter case let
-isotropic K-subspaces of V. In the latter case let 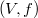 be a vector space endowed with a regular
be a vector space endowed with a regular  -hermitian form,
-hermitian form, 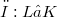 a K-linear map and
a K-linear map and 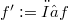 . We show that for linear groups the number of orbits depends only on the degree of the field extension and on the dimension of V. The orbits are classified completely when
. We show that for linear groups the number of orbits depends only on the degree of the field extension and on the dimension of V. The orbits are classified completely when ![[L:K]≤ 3](http://siba-ese.unile.it/plugins/generic/latexRender/cache/989b2cb68b760dd59118193fc254fa44.png) . For unitary groups in general the number of orbits depends also on the underlying fields and on the map φ. We discuss in more detail the quadratic case for some particular fields.
. For unitary groups in general the number of orbits depends also on the underlying fields and on the map φ. We discuss in more detail the quadratic case for some particular fields.
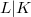 be a finite skew field extension, K commutative and V a finite dimensional vector space over L. We study the action of general L-linear groups on the set of K-subspaces of V and the action of unitary groups on the set of
be a finite skew field extension, K commutative and V a finite dimensional vector space over L. We study the action of general L-linear groups on the set of K-subspaces of V and the action of unitary groups on the set of 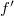 -isotropic K-subspaces of V. In the latter case let
-isotropic K-subspaces of V. In the latter case let 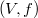 be a vector space endowed with a regular
be a vector space endowed with a regular  -hermitian form,
-hermitian form, 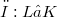 a K-linear map and
a K-linear map and 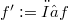 . We show that for linear groups the number of orbits depends only on the degree of the field extension and on the dimension of V. The orbits are classified completely when
. We show that for linear groups the number of orbits depends only on the degree of the field extension and on the dimension of V. The orbits are classified completely when ![[L:K]≤ 3](http://siba-ese.unile.it/plugins/generic/latexRender/cache/989b2cb68b760dd59118193fc254fa44.png) . For unitary groups in general the number of orbits depends also on the underlying fields and on the map φ. We discuss in more detail the quadratic case for some particular fields.
. For unitary groups in general the number of orbits depends also on the underlying fields and on the map φ. We discuss in more detail the quadratic case for some particular fields.DOI Code:
10.1285/i15900932v18n2p245
Keywords:
Skew field extensionCentral simple algebra; General linear group; Unitary group; Grassmann variety; Hermitean forms; Singular subspaces; Orbits
Classification:
11E57; 11E39; 12E15; 14L30; 15A03
Full Text: PDF


