The submanifolds 
of the manifold 
. II. Fundamental equations on of
Abstract
In our previous paper [4], we studied the induced connection of the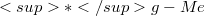 
-connection on a submanifold embedded in a manifold 
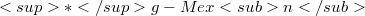together with the generalized coefficients 
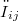of the second fundamental form of , with emphasis on the proof of a necessary and sufficient condition for the induced connection of in to be a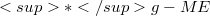 
-connection. This paper is a direct continuation of [4]. In this paper, we derive the generalized fundamental equations on of , such as the generalized Gauss formulae, the generalized Weingarten equations, and the Gauss-Codazzi equations. Furthermore, we also present surveyable tensorial representations of curvature tensors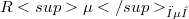 
of and 
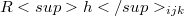of .
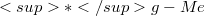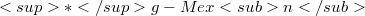-connection on a submanifold embedded in a manifold together with the generalized coefficients 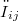of the second fundamental form of , with emphasis on the proof of a necessary and sufficient condition for the induced connection of in to be a 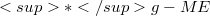-connection. This paper is a direct continuation of [4]. In this paper, we derive the generalized fundamental equations on of , such as the generalized Gauss formulae, the generalized Weingarten equations, and the Gauss-Codazzi equations. 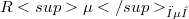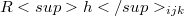Furthermore, we also present surveyable tensorial representations of curvature tensors of and of .DOI Code:
10.1285/i15900932v18n2p227
Full Text: PDF
