The submanifolds 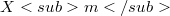 of the manifold
of the manifold  . I. The induced connection on
. I. The induced connection on  of
of 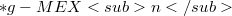
Abstract
An Einstein's connection which takes the form (2.33) is called an 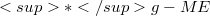 -connection. Recently, Chung and et al ([15], 1993)introduced a new manifolds, called an n-dimensional
-connection. Recently, Chung and et al ([15], 1993)introduced a new manifolds, called an n-dimensional 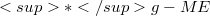 -manifold (debnoted by
-manifold (debnoted by  ).The manifold
).The manifold  is a generalized n-dimensional Riemannian manifold
is a generalized n-dimensional Riemannian manifold 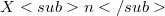 on which the differential geometric structure is imposed by the unified field tensor
on which the differential geometric structure is imposed by the unified field tensor 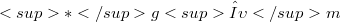 satisfying certain conditions through the
satisfying certain conditions through the 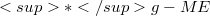 -connection. In the following series of two papers, we investigate the submanifolds
-connection. In the following series of two papers, we investigate the submanifolds  of
of  : I. The induced connection on
: I. The induced connection on  of
of  II. The generalized fundamental equations on
II. The generalized fundamental equations on  of
of  In this paper, Part I of the series, we present a brief introduction of n-dimensional
In this paper, Part I of the series, we present a brief introduction of n-dimensional 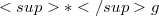 -unified field theory, the C-nonholonomic frame of reference in
-unified field theory, the C-nonholonomic frame of reference in 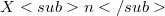 at points of
at points of 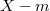 , and the manifold
, and the manifold  . and then, we introduce the generalized coefficients of the second fundamental form of
. and then, we introduce the generalized coefficients of the second fundamental form of  and prove a necessary and sufficient condition for the induced connection on
and prove a necessary and sufficient condition for the induced connection on  of
of 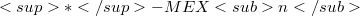 to be a
to be a 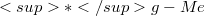 -connection. Our subsequent paper, Part II of the series, deals with the generalized fundamental equations on
-connection. Our subsequent paper, Part II of the series, deals with the generalized fundamental equations on  of
of 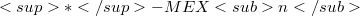 , such as the generalized Gauss formulae, the generalized Weingarten equations, and the Gauss-Codazzi equations.
, such as the generalized Gauss formulae, the generalized Weingarten equations, and the Gauss-Codazzi equations.
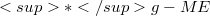 -connection. Recently, Chung and et al ([15], 1993)introduced a new manifolds, called an n-dimensional
-connection. Recently, Chung and et al ([15], 1993)introduced a new manifolds, called an n-dimensional 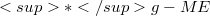 -manifold (debnoted by
-manifold (debnoted by  ).The manifold
).The manifold  is a generalized n-dimensional Riemannian manifold
is a generalized n-dimensional Riemannian manifold 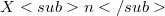 on which the differential geometric structure is imposed by the unified field tensor
on which the differential geometric structure is imposed by the unified field tensor 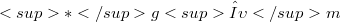 satisfying certain conditions through the
satisfying certain conditions through the 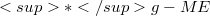 -connection. In the following series of two papers, we investigate the submanifolds
-connection. In the following series of two papers, we investigate the submanifolds  of
of  : I. The induced connection on
: I. The induced connection on  of
of  II. The generalized fundamental equations on
II. The generalized fundamental equations on  of
of  In this paper, Part I of the series, we present a brief introduction of n-dimensional
In this paper, Part I of the series, we present a brief introduction of n-dimensional 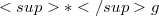 -unified field theory, the C-nonholonomic frame of reference in
-unified field theory, the C-nonholonomic frame of reference in 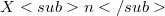 at points of
at points of 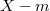 , and the manifold
, and the manifold  . and then, we introduce the generalized coefficients of the second fundamental form of
. and then, we introduce the generalized coefficients of the second fundamental form of  and prove a necessary and sufficient condition for the induced connection on
and prove a necessary and sufficient condition for the induced connection on  of
of 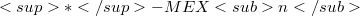 to be a
to be a 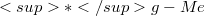 -connection. Our subsequent paper, Part II of the series, deals with the generalized fundamental equations on
-connection. Our subsequent paper, Part II of the series, deals with the generalized fundamental equations on  of
of 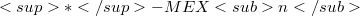 , such as the generalized Gauss formulae, the generalized Weingarten equations, and the Gauss-Codazzi equations.
, such as the generalized Gauss formulae, the generalized Weingarten equations, and the Gauss-Codazzi equations.DOI Code:
10.1285/i15900932v18n2p213
Full Text: PDF


