A supplement to the Alexandrov–Lester Theorem
Abstract
Let 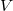 be the 4-dimensional Minkowski-space of special relativity over the reals with quadratic form Q. Consider a mapping
be the 4-dimensional Minkowski-space of special relativity over the reals with quadratic form Q. Consider a mapping 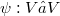 such that
such that 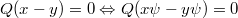 for all
for all 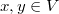 . Under the assumption that
. Under the assumption that 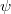 is a bijection Alexandrov's theorem states that
is a bijection Alexandrov's theorem states that 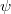 is a linear bijection followed by a translation. Our results imply (as a special case) that the assumption of
is a linear bijection followed by a translation. Our results imply (as a special case) that the assumption of 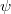 being a bijection an be dropped.
being a bijection an be dropped.
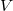 be the 4-dimensional Minkowski-space of special relativity over the reals with quadratic form Q. Consider a mapping
be the 4-dimensional Minkowski-space of special relativity over the reals with quadratic form Q. Consider a mapping 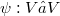 such that
such that 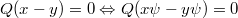 for all
for all 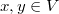 . Under the assumption that
. Under the assumption that 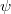 is a bijection Alexandrov's theorem states that
is a bijection Alexandrov's theorem states that 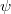 is a linear bijection followed by a translation. Our results imply (as a special case) that the assumption of
is a linear bijection followed by a translation. Our results imply (as a special case) that the assumption of 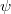 being a bijection an be dropped.
being a bijection an be dropped.DOI Code:
10.1285/i15900932v21n2p35
Keywords:
Distance-preserving mappings; Collineations; Orthogonal groups; Special relativity
Classification:
51N30; 51F25; 83A05; 51M05; 51P05
Full Text: PDF


