An overview on Laakso spaces
Abstract
Laakso's construction is a famous example of an Ahlfors 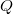 -regular metric measure space admitting a weak
-regular metric measure space admitting a weak 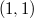 -Poincare inequality that can not be embedded in
-Poincare inequality that can not be embedded in 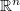 for any
for any 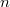 . The construction is of particular interest because it works for any fixed dimension
. The construction is of particular interest because it works for any fixed dimension 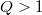 , even fractional ones. In this paper we will shed some light on Laakso's work by expanding some of his statements and proving results that were left unproved in the original paper.
, even fractional ones. In this paper we will shed some light on Laakso's work by expanding some of his statements and proving results that were left unproved in the original paper.
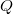 -regular metric measure space admitting a weak
-regular metric measure space admitting a weak  -Poincare inequality that can not be embedded in
-Poincare inequality that can not be embedded in 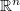 for any
for any 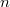 . The construction is of particular interest because it works for any fixed dimension
. The construction is of particular interest because it works for any fixed dimension 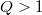 , even fractional ones. In this paper we will shed some light on Laakso's work by expanding some of his statements and proving results that were left unproved in the original paper.
, even fractional ones. In this paper we will shed some light on Laakso's work by expanding some of his statements and proving results that were left unproved in the original paper.DOI Code:
10.1285/i15900932v44n2p53
Keywords:
Laakso Space; Geodesics
Full Text: PDF


