Hypergeometric series, lemniscate functions, 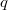 -extensions and Jacobi elliptic functions
-extensions and Jacobi elliptic functions
Abstract
In this paper, we provide a solution to an open problem posed by Campbell and Chu [12] concerning the explicit evaluation of a constant known as the 'lemniscate-like constant.' We demonstrate that by utilizing tools related to the primary Jacobi elliptic functions, we can derive a closed-form expression in terms of 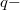 generalizations of Zeta and Polylogarithm functions and well-known mathematical constants. Lastly, we establish that our primary outcome establishes a non-obvious connection between various and disparate mathematical entities.
generalizations of Zeta and Polylogarithm functions and well-known mathematical constants. Lastly, we establish that our primary outcome establishes a non-obvious connection between various and disparate mathematical entities.
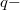 generalizations of Zeta and Polylogarithm functions and well-known mathematical constants. Lastly, we establish that our primary outcome establishes a non-obvious connection between various and disparate mathematical entities.
generalizations of Zeta and Polylogarithm functions and well-known mathematical constants. Lastly, we establish that our primary outcome establishes a non-obvious connection between various and disparate mathematical entities.DOI Code:
10.1285/i15900932v44n2p1
Keywords:
Closed forms; hypergeometric functions; Jacobi elliptic functions; q-Zeta and q-Polylogarithm functions; lemniscate functions
Full Text: PDF


