Counting the generalized twisted fields
Abstract
In this paper we exploit a theorem of Biliotti, Jha, and Johnson exhibiting a
procedure to count the number of non- isotopic generalized twisted fields of orders 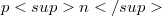 where
where 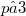 which is denoted by
which is denoted by 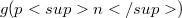 .We show that
.We show that 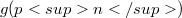 is a polynomial in p that is sharply bounded below by
is a polynomial in p that is sharply bounded below by 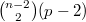 and bounded above by a polynomial of degree
and bounded above by a polynomial of degree 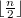 .
.
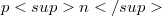 where
where 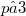 which is denoted by
which is denoted by 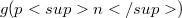 .We show that
.We show that 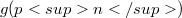 is a polynomial in p that is sharply bounded below by
is a polynomial in p that is sharply bounded below by 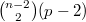 and bounded above by a polynomial of degree
and bounded above by a polynomial of degree 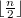 .
.DOI Code:
10.1285/i15900932v27n1p53
Keywords:
Semifield; Generalized twisted field; Projective plane; Finite geometry
Full Text: PDF PS


