On groups with many subgroups satisfying a transitive normality relation
Abstract
A group  is said to be a
is said to be a 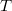 -group if normality in
-group if normality in  is a transitive relation. Clearly, as a simple group has the property
is a transitive relation. Clearly, as a simple group has the property 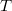 , it follows that
, it follows that 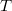 is not subgroup closed. A group
is not subgroup closed. A group  is called a
is called a 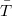 -group if all its subgroups are
-group if all its subgroups are 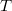 -groups. In this note the structure of groups all of whose (proper) subgroups either are nilpotent or satisfy the property
-groups. In this note the structure of groups all of whose (proper) subgroups either are nilpotent or satisfy the property 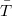 will be investigated.
will be investigated.
 is said to be a
is said to be a 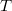 -group if normality in
-group if normality in  is a transitive relation. Clearly, as a simple group has the property
is a transitive relation. Clearly, as a simple group has the property 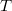 , it follows that
, it follows that 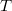 is not subgroup closed. A group
is not subgroup closed. A group  is called a
is called a 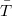 -group if all its subgroups are
-group if all its subgroups are 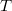 -groups. In this note the structure of groups all of whose (proper) subgroups either are nilpotent or satisfy the property
-groups. In this note the structure of groups all of whose (proper) subgroups either are nilpotent or satisfy the property 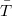 will be investigated.
will be investigated.DOI Code:
10.1285/i15900932v44n1p45
Keywords:
$T$-group; nilpotent group; Fitting subgroup
Full Text: PDF


