The uniqueness of a fixed degree singular plane model
Abstract
Let 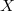 be the normalization of an integral degree
be the normalization of an integral degree 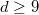 plane curve
plane curve 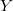 . We prove that
. We prove that 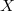 has a unique
has a unique 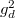 if
if 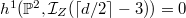 , where
, where 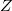 is the conductor of
is the conductor of 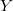 . Moreover,
. Moreover, 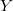 is the unique plane model of
is the unique plane model of 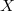 of degree at most
of degree at most 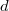 .
.
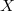 be the normalization of an integral degree
be the normalization of an integral degree 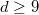 plane curve
plane curve 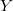 . We prove that
. We prove that 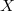 has a unique
has a unique 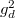 if
if 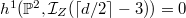 , where
, where 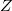 is the conductor of
is the conductor of 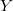 . Moreover,
. Moreover, 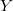 is the unique plane model of
is the unique plane model of 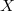 of degree at most
of degree at most 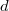 .
.DOI Code:
10.1285/i15900932v44n1p21
Keywords:
plane curve; uniqueness of a plane model
Full Text: PDF


