Involution semi-braces and the Yang-Baxter equation
Abstract
The main aim of this paper is to provide set-theoretical solutions of the Yang-Baxter equation that are not necessarily bijective. We use the new structure of involution semi-brace, that is a quadruple 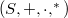 with
with 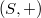 a semigroup and
a semigroup and 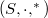 an involution semigroup satisfying the relation
an involution semigroup satisfying the relation 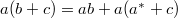 , for all
, for all 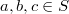 .
.
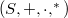 with
with 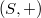 a semigroup and
a semigroup and 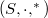 an involution semigroup satisfying the relation
an involution semigroup satisfying the relation 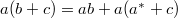 , for all
, for all 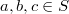 .
.DOI Code:
10.1285/i15900932v42n2p63
Keywords:
semi-brace; set-theoretical solution; Yang-Baxter equation; involution
Full Text: PDF


