 -Ricci soliton on GSSF with Sasakian metric
-Ricci soliton on GSSF with Sasakian metric
Abstract
We study generalized Sasakian-space-forms (GSSF) 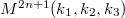 with Sasa\-kian metric admitting
with Sasa\-kian metric admitting  -Ricci soliton. We obtain that either such GSSF has
-Ricci soliton. We obtain that either such GSSF has 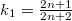 ,
, 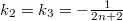 and
and  -soliton is steady or
-soliton is steady or 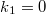 ,
, 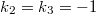 and
and  -soliton is expanding. Also, we provide some examples in support of results. Further, we give an example that GSSF with Sasakian metric with
-soliton is expanding. Also, we provide some examples in support of results. Further, we give an example that GSSF with Sasakian metric with 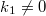 and
and 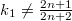 do not admit the
do not admit the  -Ricci soliton.
-Ricci soliton.
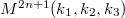 with Sasa\-kian metric admitting
with Sasa\-kian metric admitting  -Ricci soliton. We obtain that either such GSSF has
-Ricci soliton. We obtain that either such GSSF has 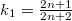 ,
, 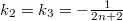 and
and  -soliton is steady or
-soliton is steady or 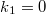 ,
, 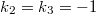 and
and  -soliton is expanding. Also, we provide some examples in support of results. Further, we give an example that GSSF with Sasakian metric with
-soliton is expanding. Also, we provide some examples in support of results. Further, we give an example that GSSF with Sasakian metric with 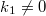 and
and 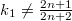 do not admit the
do not admit the  -Ricci soliton.
-Ricci soliton.DOI Code:
10.1285/i15900932v42n1p95
Keywords:
*-Ricci soliton; Generalized Sasakian-space-forms; Sasakian manifolds; Positive-Sasakian; Null-Sasakian
Full Text: PDF


