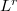 inequalities for the derivative of a polynomial
inequalities for the derivative of a polynomial
Abstract
Let 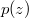 be a polynomial of degree
be a polynomial of degree 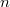 having no zero in
having no zero in 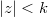 ,
, 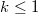 , then Govil [Proc. Nat. Acad. Sci.,
, then Govil [Proc. Nat. Acad. Sci., 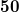 , (1980), 50-52] proved
, (1980), 50-52] proved
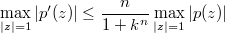 ,
,
provided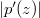 and
and 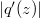 attain their maxima at the same point on the circle
attain their maxima at the same point on the circle 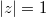 , where
, where
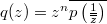 .
.
In this paper, we not only obtain an integral mean inequality for the above inequality but also extend an improved version of it into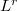 norm.
norm.
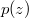 be a polynomial of degree
be a polynomial of degree 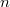 having no zero in
having no zero in 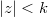 ,
, 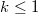 , then Govil [Proc. Nat. Acad. Sci.,
, then Govil [Proc. Nat. Acad. Sci., 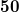 , (1980), 50-52] proved
, (1980), 50-52] proved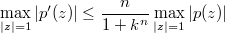 ,
, provided
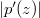 and
and 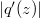 attain their maxima at the same point on the circle
attain their maxima at the same point on the circle 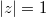 , where
, where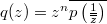 .
. In this paper, we not only obtain an integral mean inequality for the above inequality but also extend an improved version of it into
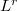 norm.
norm.DOI Code:
10.1285/i15900932v41n2p19
Keywords:
Inequalities; Polynomials; Zeros; Maximum modulus; Lr norm
Full Text: PDF


