Existence and approximation of solutions for a class of degenerate elliptic equations with Neumann boundary condition
Abstract
In this work we study the equation 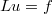 , where
, where  is a degenerate elliptic operator, with Neumann boundary condition in a bounded open set
is a degenerate elliptic operator, with Neumann boundary condition in a bounded open set 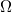 . We prove the existence and uniqueness of weak solutions in the weighted Sobolev space
. We prove the existence and uniqueness of weak solutions in the weighted Sobolev space 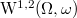 for the Neumann problem. The main result establishes that a weak solution of degenerate elliptic equations can be approximated by a sequence of solutions for non-degenerate elliptic equations
for the Neumann problem. The main result establishes that a weak solution of degenerate elliptic equations can be approximated by a sequence of solutions for non-degenerate elliptic equations
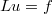 , where
, where  is a degenerate elliptic operator, with Neumann boundary condition in a bounded open set
is a degenerate elliptic operator, with Neumann boundary condition in a bounded open set 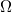 . We prove the existence and uniqueness of weak solutions in the weighted Sobolev space
. We prove the existence and uniqueness of weak solutions in the weighted Sobolev space 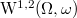 for the Neumann problem. The main result establishes that a weak solution of degenerate elliptic equations can be approximated by a sequence of solutions for non-degenerate elliptic equations
for the Neumann problem. The main result establishes that a weak solution of degenerate elliptic equations can be approximated by a sequence of solutions for non-degenerate elliptic equationsDOI Code:
10.1285/i15900932v40n2p63
Keywords:
Neumann problem; weighted Sobolev spaces
Full Text: PDF


