Second cohomology of multiplicative Lie rings and Schreier's extension theory
Abstract
Our goal of this paper is to develop an analogue of the theory of group extensions for multiplicative Lie rings. We first define a factor system of pair of multiplicative Lie rings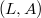 
, which use to construct an extension of 
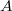by 
. Then we state Schreier's theorem for multiplicative Lie rings. We also use this notation to introduce second cohomology group of multiplicative Lie rings. Finally, we show that the equivalence classes of multiplicative Lie ring extensions can be identified with second cohomology group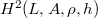 
, where acts on 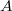by 
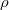and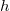 
.
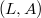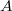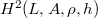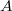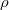, which use to construct an extension of by . Then we state Schreier's theorem for multiplicative Lie rings. We also use this notation to introduce second cohomology group of multiplicative Lie rings. Finally, we show that the equivalence classes of multiplicative Lie ring extensions can be identified with second cohomology group , where acts on by and 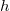.DOI Code:
10.1285/i15900932v40n2p37
Keywords:
Multiplicative Lie ring; extension of multiplicative Lie ring; second cohomology group of multiplicative Lie ring and factor system
Full Text: PDF
