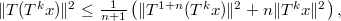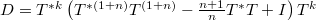On 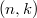 -quasi class
-quasi class 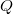 Operators
Operators
Abstract
Let 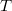 be a bounded linear operator on a complex Hilbert space
be a bounded linear operator on a complex Hilbert space 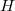 . In this paper we introduce a new class of operators:
. In this paper we introduce a new class of operators: 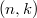 -quasi class
-quasi class 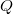 operators, superclass of
operators, superclass of 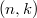 -quasi paranormal operators. An operator
-quasi paranormal operators. An operator 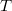 is said to be
is said to be 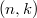 -quasi class
-quasi class 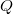 if it satisfies
if it satisfies 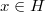 and for some nonnegative integers
and for some nonnegative integers 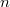 and
and 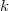 . We prove the basic structural properties of this class of operators. It will be proved that If
. We prove the basic structural properties of this class of operators. It will be proved that If 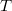 has a no non-trivial invariant subspace, then the nonnegative operator
has a no non-trivial invariant subspace, then the nonnegative operator 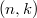 -quasi class
-quasi class 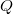 does not have SVEP property. In the last section we also characterize the
does not have SVEP property. In the last section we also characterize the 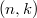 -quasi class
-quasi class 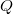 composition operators on Fock spaces.
composition operators on Fock spaces.
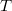 be a bounded linear operator on a complex Hilbert space
be a bounded linear operator on a complex Hilbert space 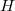 . In this paper we introduce a new class of operators:
. In this paper we introduce a new class of operators: 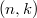 -quasi class
-quasi class 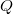 operators, superclass of
operators, superclass of 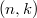 -quasi paranormal operators. An operator
-quasi paranormal operators. An operator 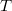 is said to be
is said to be 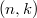 -quasi class
-quasi class 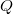 if it satisfies
if it satisfies for all
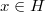 and for some nonnegative integers
and for some nonnegative integers 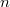 and
and 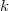 . We prove the basic structural properties of this class of operators. It will be proved that If
. We prove the basic structural properties of this class of operators. It will be proved that If 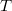 has a no non-trivial invariant subspace, then the nonnegative operator
has a no non-trivial invariant subspace, then the nonnegative operator is a strongly stable contraction. In section 4, we give some examples which compare our class with other known classes of operators and as a consequence we prove that
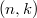 -quasi class
-quasi class 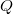 does not have SVEP property. In the last section we also characterize the
does not have SVEP property. In the last section we also characterize the 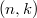 -quasi class
-quasi class 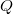 composition operators on Fock spaces.
composition operators on Fock spaces.DOI Code:
10.1285/i15900932v39n2p39
Keywords:
$(n,k)$-quasi class $Q$; $(n,k)$-quasi paranormal operators; SVEP property; Fock space; composition operators
Full Text: PDF