Lie algebra representations and 2-index 4-variable 1-parameter Hermite polynomials
Abstract
This paper is an attempt to stress the usefulness of multi-variable special functions by expressing them in terms of the corresponding Lie algebra or Lie group. The problem of framing the 2-index 4-variable 1-parameter Hermite polynomials (2I4V1PHP) into the context of the irreducible representations 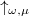 of
of 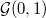 and
and 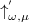 of
of 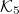 is considered. Certain relations involving 2I4V1PHP
is considered. Certain relations involving 2I4V1PHP 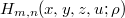 are obtained using the approach adopted by Miller. Certain examples involving other forms of Hermite polynomials are derived as special cases. Further, some properties of the 2I4V1PHP
are obtained using the approach adopted by Miller. Certain examples involving other forms of Hermite polynomials are derived as special cases. Further, some properties of the 2I4V1PHP 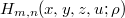 are obtained by using a quadratic combination of four operators defined on a Lie algebra of endomorphisms of a vector space.
are obtained by using a quadratic combination of four operators defined on a Lie algebra of endomorphisms of a vector space.
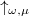 of
of 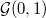 and
and 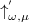 of
of 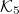 is considered. Certain relations involving 2I4V1PHP
is considered. Certain relations involving 2I4V1PHP 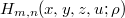 are obtained using the approach adopted by Miller. Certain examples involving other forms of Hermite polynomials are derived as special cases. Further, some properties of the 2I4V1PHP
are obtained using the approach adopted by Miller. Certain examples involving other forms of Hermite polynomials are derived as special cases. Further, some properties of the 2I4V1PHP 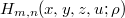 are obtained by using a quadratic combination of four operators defined on a Lie algebra of endomorphisms of a vector space.
are obtained by using a quadratic combination of four operators defined on a Lie algebra of endomorphisms of a vector space.DOI Code:
10.1285/i15900932v39n1p65
Keywords:
2-index 4-variable 1-parameter Hermite polynomials; Lie group; Lie algebra; representation theory; implicit formulae
Full Text: PDF


