A Bogomolov type property relative to a normalized height on 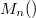
Abstract
In \cite{Tala 99}, Talamanca introduced a normalized height on 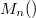 , which is an analogue of the canonical height on elliptic curves. In this paper, we examine whether
, which is an analogue of the canonical height on elliptic curves. In this paper, we examine whether 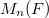 has a Bogomolov type property relative to this height if a subfield
has a Bogomolov type property relative to this height if a subfield 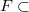 has the Bogomolov property.
has the Bogomolov property.
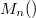 , which is an analogue of the canonical height on elliptic curves. In this paper, we examine whether
, which is an analogue of the canonical height on elliptic curves. In this paper, we examine whether 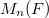 has a Bogomolov type property relative to this height if a subfield
has a Bogomolov type property relative to this height if a subfield 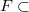 has the Bogomolov property.
has the Bogomolov property.DOI Code:
10.1285/i15900932v39n1p59
Keywords:
normalized height on $M_n(\masaoQB)$; Bogomolov property
Full Text: PDF


