On a perturbation of a class of Schr"odinger systems in 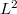 -spaces
-spaces
Abstract
The aim of this short note is to prove a generation result of 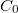 -semigroups in
-semigroups in 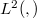 , with the characterization of the domain of their generators, for a perturbation of a class of matrix Schr"odinger operators by symmetric potential matrices whose entries can grow exponentially at infinity. A further perturbation by drift matrices with entries that can grow at most linearly at infinity, is considered. Finally, suitable assumptions which guarantee that the generated semigroups are analytic, are provided too.
, with the characterization of the domain of their generators, for a perturbation of a class of matrix Schr"odinger operators by symmetric potential matrices whose entries can grow exponentially at infinity. A further perturbation by drift matrices with entries that can grow at most linearly at infinity, is considered. Finally, suitable assumptions which guarantee that the generated semigroups are analytic, are provided too.
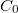 -semigroups in
-semigroups in 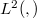 , with the characterization of the domain of their generators, for a perturbation of a class of matrix Schr"odinger operators by symmetric potential matrices whose entries can grow exponentially at infinity. A further perturbation by drift matrices with entries that can grow at most linearly at infinity, is considered. Finally, suitable assumptions which guarantee that the generated semigroups are analytic, are provided too.
, with the characterization of the domain of their generators, for a perturbation of a class of matrix Schr"odinger operators by symmetric potential matrices whose entries can grow exponentially at infinity. A further perturbation by drift matrices with entries that can grow at most linearly at infinity, is considered. Finally, suitable assumptions which guarantee that the generated semigroups are analytic, are provided too.DOI Code:
10.1285/i15900932v38n2p125
Keywords:
Matrix Schr\"odinger operators; characterization of the domain; perturbation theory; analytic semigroups
Full Text: PDF


