Derivation subalgebras of Lie algebras
Abstract
Let  be a Lie algebra and
be a Lie algebra and 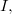
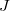 be two ideals of
be two ideals of  . If
. If 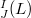 denotes the set of all derivations of
denotes the set of all derivations of  whose images are in
whose images are in 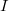 and send
and send 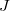 to zero, then we give necessary and sufficient conditions under which
to zero, then we give necessary and sufficient conditions under which 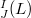 is equal to some special subalgebras of the derivation algebra of
is equal to some special subalgebras of the derivation algebra of  . We also consider finite dimensional Lie algebra for which the center of the set of inner derivations,
. We also consider finite dimensional Lie algebra for which the center of the set of inner derivations, 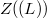 , is equal to the set of central derivations of
, is equal to the set of central derivations of  ,
, 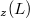 , and give a characterisation of such Lie algebras.
, and give a characterisation of such Lie algebras.
 be a Lie algebra and
be a Lie algebra and 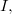
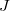 be two ideals of
be two ideals of  . If
. If 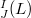 denotes the set of all derivations of
denotes the set of all derivations of  whose images are in
whose images are in 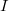 and send
and send 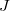 to zero, then we give necessary and sufficient conditions under which
to zero, then we give necessary and sufficient conditions under which 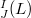 is equal to some special subalgebras of the derivation algebra of
is equal to some special subalgebras of the derivation algebra of  . We also consider finite dimensional Lie algebra for which the center of the set of inner derivations,
. We also consider finite dimensional Lie algebra for which the center of the set of inner derivations, 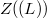 , is equal to the set of central derivations of
, is equal to the set of central derivations of  ,
, 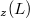 , and give a characterisation of such Lie algebras.
, and give a characterisation of such Lie algebras.DOI Code:
10.1285/i15900932v38n2p105
Keywords:
Derivation; central derivation; inner derivation
Full Text: PDF


