Duality between cuspidal butterflies and cuspidal 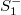 singularities on maximal surfaces
singularities on maximal surfaces
Abstract
We give criteria for cuspidal butterflies and cuspidal 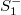 (
(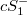 ) singularities in terms of the Weierstrass data for maximal surfaces, and also show non-existence of cuspidal
) singularities in terms of the Weierstrass data for maximal surfaces, and also show non-existence of cuspidal 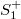 (
(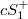 ) singularities on maximal surfaces. Moreover, we show duality between these singularities considering the conjugate maximal surfaces each other.
) singularities on maximal surfaces. Moreover, we show duality between these singularities considering the conjugate maximal surfaces each other.
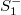 (
(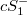 ) singularities in terms of the Weierstrass data for maximal surfaces, and also show non-existence of cuspidal
) singularities in terms of the Weierstrass data for maximal surfaces, and also show non-existence of cuspidal 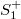 (
(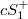 ) singularities on maximal surfaces. Moreover, we show duality between these singularities considering the conjugate maximal surfaces each other.
) singularities on maximal surfaces. Moreover, we show duality between these singularities considering the conjugate maximal surfaces each other.DOI Code:
10.1285/i15900932v38n1p115
Keywords:
maximal surface; frontal; cuspidal butterfly; cuspidal $S_k$ singularity
Full Text: PDF


