Some congruences modulo 2, 8 and 12 for Andrews' singular overpartitions
Abstract
Recently, G. E. Andrews defined combinatorial objects which he called 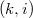 -singular overpartitions, overpartitions of
-singular overpartitions, overpartitions of 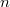 in which no part is divisible by
in which no part is divisible by 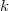 and only parts
and only parts 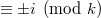 may be overlined. Let the number of
may be overlined. Let the number of 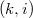 -singular overpartitions of
-singular overpartitions of 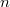 be\linebreak denoted by
be\linebreak denoted by 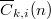 . Andrews and Chen, Hirschhorn and Sellers noted numerous congruences modulo
. Andrews and Chen, Hirschhorn and Sellers noted numerous congruences modulo 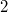 for
for 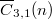 . The object of this paper is to obtain new congruences modulo
. The object of this paper is to obtain new congruences modulo 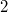 for
for 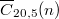 and modulo
and modulo 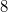 and
and 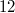 for
for 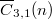 .
.
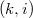 -singular overpartitions, overpartitions of
-singular overpartitions, overpartitions of 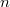 in which no part is divisible by
in which no part is divisible by 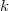 and only parts
and only parts 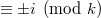 may be overlined. Let the number of
may be overlined. Let the number of 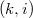 -singular overpartitions of
-singular overpartitions of 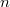 be\linebreak denoted by
be\linebreak denoted by 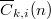 . Andrews and Chen, Hirschhorn and Sellers noted numerous congruences modulo
. Andrews and Chen, Hirschhorn and Sellers noted numerous congruences modulo 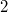 for
for 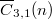 . The object of this paper is to obtain new congruences modulo
. The object of this paper is to obtain new congruences modulo 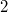 for
for 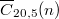 and modulo
and modulo 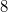 and
and 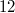 for
for 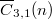 .
.DOI Code:
10.1285/i15900932v38n1p101
Keywords:
singular overpartition; congruence; generating function; sums of squares
Full Text: PDF


