On the nilpotent conjugacy class graph of groups
Abstract
The nilpotent conjugacy class graph (or NCC-graph) of a group  is a graph whose vertices are the nontrivial conjugacy classes of
is a graph whose vertices are the nontrivial conjugacy classes of  such that two distinct vertices
such that two distinct vertices 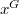 and
and 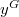 are adjacent if
are adjacent if 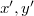 is nilpotent for some
is nilpotent for some 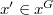 and
and 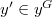 . We discuss on the number of connected components as well as diameter of connected components of these graphs. Also, we consider the induced subgraph
. We discuss on the number of connected components as well as diameter of connected components of these graphs. Also, we consider the induced subgraph 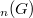 of the NCC-graph with vertices set
of the NCC-graph with vertices set 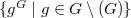 , where
, where 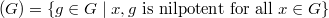 , and classify all finite non-nilpotent group
, and classify all finite non-nilpotent group  with empty and triangle-free NCC-graphs.
with empty and triangle-free NCC-graphs.
 is a graph whose vertices are the nontrivial conjugacy classes of
is a graph whose vertices are the nontrivial conjugacy classes of  such that two distinct vertices
such that two distinct vertices 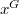 and
and 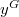 are adjacent if
are adjacent if 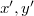 is nilpotent for some
is nilpotent for some 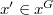 and
and 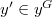 . We discuss on the number of connected components as well as diameter of connected components of these graphs. Also, we consider the induced subgraph
. We discuss on the number of connected components as well as diameter of connected components of these graphs. Also, we consider the induced subgraph 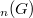 of the NCC-graph with vertices set
of the NCC-graph with vertices set 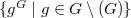 , where
, where 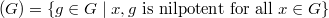 , and classify all finite non-nilpotent group
, and classify all finite non-nilpotent group  with empty and triangle-free NCC-graphs.
with empty and triangle-free NCC-graphs.DOI Code:
10.1285/i15900932v37n2p77
Keywords:
Triangle-free; conjugacy class; non-nilpotent group; graph
Full Text: PDF


