A general optimal inequality for warped product submanifolds in paracosymplectic manifolds
Abstract
The aim of this paper is to study the pseudo-Riemannian warped product submanifolds of a paracosymplectic manifold 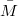 . We first, prove some fundamental lemmas and then derive some important results with parallel canonical structures on
. We first, prove some fundamental lemmas and then derive some important results with parallel canonical structures on 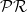 -semi-invariant submanifolds
-semi-invariant submanifolds 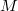 of
of 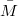 . Finally, we describe the warped product submanifold
. Finally, we describe the warped product submanifold 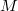 of
of 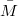 by developing the general optimal inequality in terms of warping function and squared norm of second fundamental form. We also consider the totally geodesic, mixed geodesic and equality case of the inequality.
by developing the general optimal inequality in terms of warping function and squared norm of second fundamental form. We also consider the totally geodesic, mixed geodesic and equality case of the inequality.
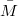 . We first, prove some fundamental lemmas and then derive some important results with parallel canonical structures on
. We first, prove some fundamental lemmas and then derive some important results with parallel canonical structures on 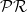 -semi-invariant submanifolds
-semi-invariant submanifolds 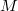 of
of 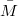 . Finally, we describe the warped product submanifold
. Finally, we describe the warped product submanifold 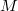 of
of 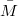 by developing the general optimal inequality in terms of warping function and squared norm of second fundamental form. We also consider the totally geodesic, mixed geodesic and equality case of the inequality.
by developing the general optimal inequality in terms of warping function and squared norm of second fundamental form. We also consider the totally geodesic, mixed geodesic and equality case of the inequality.DOI Code:
10.1285/i15900932v37n2p45
Keywords:
Paracontact manifold; Submanifold; Warped product
Full Text: PDF


