Complex geometry of real hyperboloids
Abstract
We investigate, using horospheres, the spectrum of the Laplace-Beltrami operator on pseudo hyperbolic spaces (hyperboloids), which, in general, is ultra hyperbolic. Real horospheres define only the continuous spectrum, but the discrete spectrum is connected with complex horospheres. We connect with them the horospherical Cauchy transform which acts at 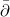 -cohomology. Correspondingly, for continuous spectrum we have an analogue of the Poisson problem with data on the real boundary but for the discrete spectrum - with cohomological data on the complex boundary.
-cohomology. Correspondingly, for continuous spectrum we have an analogue of the Poisson problem with data on the real boundary but for the discrete spectrum - with cohomological data on the complex boundary.
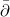 -cohomology. Correspondingly, for continuous spectrum we have an analogue of the Poisson problem with data on the real boundary but for the discrete spectrum - with cohomological data on the complex boundary.
-cohomology. Correspondingly, for continuous spectrum we have an analogue of the Poisson problem with data on the real boundary but for the discrete spectrum - with cohomological data on the complex boundary.DOI Code:
10.1285/i15900932v37suppl1p75
Keywords:
pseudo hyperbolic spaces; Laplace-Beltrami operetor; horospheres; horospherical space; complex horospheres; degenerated horospheres; horospherical transform; horospherical; Cauchy transform; $\bar{\partial}$-cohomology
Full Text: PDF


