New generalizations of lifting modules
Abstract
In this paper, we call a module 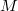 almost
almost 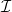 -lifting if, for any element
-lifting if, for any element 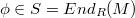 , there exists a decomposition
, there exists a decomposition 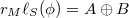 such that
such that 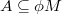 and
and 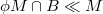 . This definition generalizes the lifting modules and left generalized semiregular rings. Some properties of these modules are investigated. We show that if
. This definition generalizes the lifting modules and left generalized semiregular rings. Some properties of these modules are investigated. We show that if 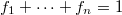 in
in 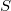 , where
, where 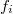
 s are orthogonal central idempotents, then
s are orthogonal central idempotents, then 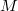 is an almost
is an almost 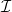 -lifting module if and only if each
-lifting module if and only if each 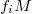 is almost
is almost 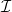 -lifting. In addition, we call a module
-lifting. In addition, we call a module 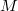
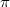 -
-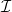 -lifting if, for any
-lifting if, for any 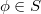 , there exists a decomposition
, there exists a decomposition 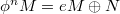 for some positive integer
for some positive integer 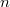 such that
such that 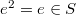 and
and 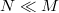 . We characterize semi-
. We characterize semi-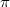 -regular rings in terms of
-regular rings in terms of 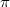 -
-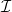 -lifting modules. Moreover, we show that if
-lifting modules. Moreover, we show that if 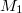 and
and 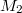 are abelian
are abelian 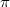 -
-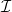 -lifting modules with
-lifting modules with 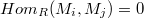 for
for 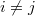 , then
, then 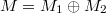 is a
is a 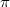 -
-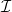 -lifting module.
-lifting module.
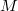 almost
almost 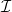 -lifting if, for any element
-lifting if, for any element 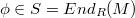 , there exists a decomposition
, there exists a decomposition 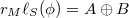 such that
such that 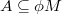 and
and 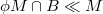 . This definition generalizes the lifting modules and left generalized semiregular rings. Some properties of these modules are investigated. We show that if
. This definition generalizes the lifting modules and left generalized semiregular rings. Some properties of these modules are investigated. We show that if 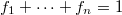 in
in 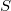 , where
, where 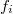
 s are orthogonal central idempotents, then
s are orthogonal central idempotents, then 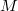 is an almost
is an almost 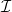 -lifting module if and only if each
-lifting module if and only if each 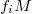 is almost
is almost 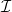 -lifting. In addition, we call a module
-lifting. In addition, we call a module 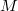
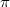 -
-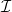 -lifting if, for any
-lifting if, for any 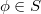 , there exists a decomposition
, there exists a decomposition 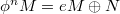 for some positive integer
for some positive integer 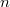 such that
such that 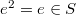 and
and 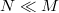 . We characterize semi-
. We characterize semi-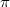 -regular rings in terms of
-regular rings in terms of 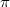 -
-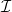 -lifting modules. Moreover, we show that if
-lifting modules. Moreover, we show that if 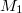 and
and 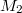 are abelian
are abelian 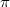 -
-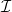 -lifting modules with
-lifting modules with 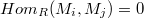 for
for 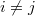 , then
, then 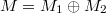 is a
is a 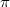 -
-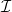 -lifting module.
-lifting module.DOI Code:
10.1285/i15900932v36n2p49
Keywords:
Lifting module; $\mathcal{I}$-Lifting module; Semiregular ring; Semi-$\pi$-regular ring
Full Text: PDF


