Geometric characterization of the rotation centers of a particle in a flow
Abstract
We provide a geometrical characterization of the instantaneous rotation centers 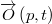 of a particle in a flow
of a particle in a flow 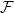 over time
over time 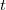 . Specifically, we will prove that: a) at a specific instant
. Specifically, we will prove that: a) at a specific instant 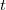 , the point
, the point 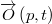 is the center of curvature at the vertex of the parabola which best fits the path-particle line
is the center of curvature at the vertex of the parabola which best fits the path-particle line 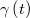 on its Darboux plane at
on its Darboux plane at  , and b) over time
, and b) over time 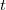 , the geometrical locus of
, the geometrical locus of 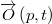 is the line of striction of the principal normal surface generated by
is the line of striction of the principal normal surface generated by 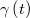 .
.
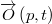 of a particle in a flow
of a particle in a flow 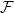 over time
over time 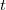 . Specifically, we will prove that: a) at a specific instant
. Specifically, we will prove that: a) at a specific instant 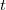 , the point
, the point 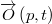 is the center of curvature at the vertex of the parabola which best fits the path-particle line
is the center of curvature at the vertex of the parabola which best fits the path-particle line 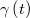 on its Darboux plane at
on its Darboux plane at  , and b) over time
, and b) over time 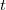 , the geometrical locus of
, the geometrical locus of 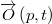 is the line of striction of the principal normal surface generated by
is the line of striction of the principal normal surface generated by 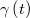 .
.DOI Code:
10.1285/i15900932v36n2p37
Keywords:
Geometry of flows; structure of flows
Full Text: PDF


