The influence of minimal subgroups on saturated fusion systems
Abstract
Let 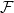 be a saturated fusion system over a \py group
be a saturated fusion system over a \py group 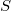 . In this paper, we investigate the influence of the minimal subgroups in
. In this paper, we investigate the influence of the minimal subgroups in 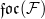 , the focal subgroup of
, the focal subgroup of 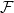 . Our main result is that if for each cyclic subgroup
. Our main result is that if for each cyclic subgroup 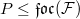 of order
of order 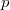 (of order
(of order 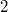 and
and 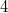 if
if 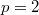 ) and each
) and each 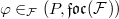 ,
, 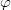 extends to an automorphism of
extends to an automorphism of 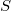 , then
, then 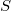 is normal in
is normal in 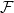 . We also give several applications of this result
. We also give several applications of this result
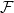 be a saturated fusion system over a \py group
be a saturated fusion system over a \py group 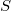 . In this paper, we investigate the influence of the minimal subgroups in
. In this paper, we investigate the influence of the minimal subgroups in 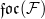 , the focal subgroup of
, the focal subgroup of 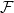 . Our main result is that if for each cyclic subgroup
. Our main result is that if for each cyclic subgroup 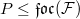 of order
of order 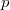 (of order
(of order 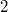 and
and 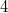 if
if 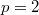 ) and each
) and each 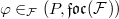 ,
, 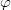 extends to an automorphism of
extends to an automorphism of 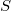 , then
, then 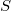 is normal in
is normal in 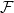 . We also give several applications of this result
. We also give several applications of this resultDOI Code:
10.1285/i15900932v36suppl1p91
Keywords:
saturated fusion system; focal subgroup; resistant group
Full Text: PDF


