Abstract differential calculus
Abstract
We consider differentiable maps in the framework of Abstract Differential Geometry and we prove a number of calculus-type results pertaining to the chain rule, restrictions of differentiable maps to subspaces, and the differentiability of maps to and from cartesian products of spaces. We elaborate the latter in the case of functional structure sheaves to obtain a situation similar to that of smooth manifolds. Since the 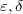 -approach does not make sense here, our machinery is the existence of a number of limits in the category of differential triads
-approach does not make sense here, our machinery is the existence of a number of limits in the category of differential triads
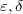 -approach does not make sense here, our machinery is the existence of a number of limits in the category of differential triads
-approach does not make sense here, our machinery is the existence of a number of limits in the category of differential triadsKeywords:
differential triad; morphism of differential triads; product; projective system; projective limit; direct sum
Full Text: PDF


