Zero-dimensional subschemes of projective spaces related to double points of linear subspaces and to fattening directions
Abstract
Fix a linear subspace 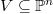 and a linearly independent set
and a linearly independent set 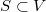 . Let
. Let 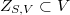 or
or 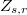 with
with 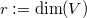 and
and 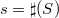 , be the zero-dimensional subscheme of
, be the zero-dimensional subscheme of 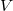 union of all double points
union of all double points 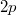 ,
, 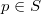 , of
, of 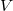 (not of
(not of 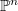 if
if 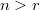 ). We study the Hilbert function of
). We study the Hilbert function of 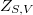 and of general unions in
and of general unions in 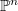 of these schemes. In characteristic
of these schemes. In characteristic 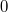 we determine the Hilbert function of general unions of
we determine the Hilbert function of general unions of 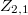 (easy), of
(easy), of 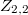 and, if
and, if 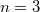 , general unions of schemes
, general unions of schemes 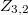 and
and 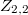
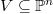 and a linearly independent set
and a linearly independent set 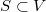 . Let
. Let 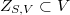 or
or 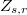 with
with 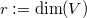 and
and 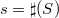 , be the zero-dimensional subscheme of
, be the zero-dimensional subscheme of 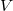 union of all double points
union of all double points 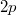 ,
, 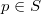 , of
, of 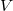 (not of
(not of 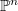 if
if 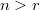 ). We study the Hilbert function of
). We study the Hilbert function of 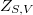 and of general unions in
and of general unions in 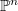 of these schemes. In characteristic
of these schemes. In characteristic 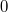 we determine the Hilbert function of general unions of
we determine the Hilbert function of general unions of 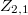 (easy), of
(easy), of 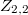 and, if
and, if 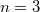 , general unions of schemes
, general unions of schemes 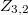 and
and 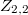
Keywords:
zero-dimensional scheme; Hilbert function; postulation
Full Text: PDF


