Sui q-archi completi in piani non desarguesiani di ordine q dispari
Abstract
By a well know theorem of Segre [5] and G. Tallini [7], the q-arcs of the desarguesian plane 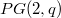 , are not complete.In [1],[2],[3] it is shown that this theorem cannot be extended to any non-desarguesian plane.In this paper, the following theorem is proved: Let
, are not complete.In [1],[2],[3] it is shown that this theorem cannot be extended to any non-desarguesian plane.In this paper, the following theorem is proved: Let  be a complete q-arc of a projective plane 𝜋 of order q. Denote by
be a complete q-arc of a projective plane 𝜋 of order q. Denote by 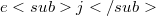 the number of those points P of 𝜋 for which the number of tangents of
the number of those points P of 𝜋 for which the number of tangents of  passing through P is j. Then
passing through P is j. Then 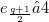 when
when 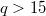 ;
; 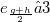 for
for 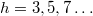 .
.
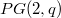 , are not complete.In [1],[2],[3] it is shown that this theorem cannot be extended to any non-desarguesian plane.In this paper, the following theorem is proved: Let
, are not complete.In [1],[2],[3] it is shown that this theorem cannot be extended to any non-desarguesian plane.In this paper, the following theorem is proved: Let  be a complete q-arc of a projective plane 𝜋 of order q. Denote by
be a complete q-arc of a projective plane 𝜋 of order q. Denote by 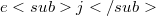 the number of those points P of 𝜋 for which the number of tangents of
the number of those points P of 𝜋 for which the number of tangents of  passing through P is j. Then
passing through P is j. Then 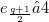 when
when 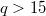 ;
; 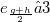 for
for 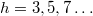 .
.DOI Code:
10.1285/i15900932v3n1p149
Full Text: PDF


