From absolute to affine geometry in terms of point-reections, midpoints, and collinearity
Abstract
We investigate equational theories expressed in terms of the point-reflection operation 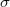 and the midpoint operation
and the midpoint operation 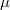 that lie strictly between the absolute and the affine theory, proving a number of dependencies and independencies in the process. Several universal theories enlarged with the collinearity predicate also lie strictly between the absolute and the affine theory. The independence models and several proofs were obtained by {\tt Tipi}, an aggregate of automatic theorem provers. To show that no set of equations with at most three variables can axiomatize the affine theory is left as an open problem.
that lie strictly between the absolute and the affine theory, proving a number of dependencies and independencies in the process. Several universal theories enlarged with the collinearity predicate also lie strictly between the absolute and the affine theory. The independence models and several proofs were obtained by {\tt Tipi}, an aggregate of automatic theorem provers. To show that no set of equations with at most three variables can axiomatize the affine theory is left as an open problem.
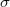 and the midpoint operation
and the midpoint operation 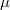 that lie strictly between the absolute and the affine theory, proving a number of dependencies and independencies in the process. Several universal theories enlarged with the collinearity predicate also lie strictly between the absolute and the affine theory. The independence models and several proofs were obtained by {\tt Tipi}, an aggregate of automatic theorem provers. To show that no set of equations with at most three variables can axiomatize the affine theory is left as an open problem.
that lie strictly between the absolute and the affine theory, proving a number of dependencies and independencies in the process. Several universal theories enlarged with the collinearity predicate also lie strictly between the absolute and the affine theory. The independence models and several proofs were obtained by {\tt Tipi}, an aggregate of automatic theorem provers. To show that no set of equations with at most three variables can axiomatize the affine theory is left as an open problem.DOI Code:
10.1285/i15900932v36n1p11
Keywords:
point-re ections; midpoints; collinearity; a ne geometry; axioms; independence; automatic theorem proving
Full Text: PDF


