Baire properties of (LF)-spaces
Abstract
We relate the study of (LF)–spaces with some covering properties of locally convex spaces, which are variations of the theme of "Baire Space". All (LF)-spaces are partitioned into theree classes, called 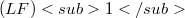 ,
, 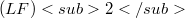 and
and 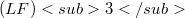 -spaces respectively. We then show that these classes are precisely the classes of
-spaces respectively. We then show that these classes are precisely the classes of 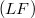 -spaces that distinguish between the several Baire-type coverings we considered.The role of the sequence space φ in this context is studied.The interaction between
-spaces that distinguish between the several Baire-type coverings we considered.The role of the sequence space φ in this context is studied.The interaction between 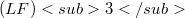 -spaces and the Separable Quotient Problem is also discussed.
-spaces and the Separable Quotient Problem is also discussed.
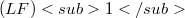 ,
, 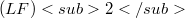 and
and 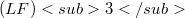 -spaces respectively. We then show that these classes are precisely the classes of
-spaces respectively. We then show that these classes are precisely the classes of 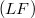 -spaces that distinguish between the several Baire-type coverings we considered.The role of the sequence space φ in this context is studied.The interaction between
-spaces that distinguish between the several Baire-type coverings we considered.The role of the sequence space φ in this context is studied.The interaction between 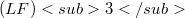 -spaces and the Separable Quotient Problem is also discussed.
-spaces and the Separable Quotient Problem is also discussed.DOI Code:
10.1285/i15900932v7n1p1
Full Text: PDF


