On natural reductivity of five-dimensional commutative spaces
Abstract
The naturally reductive homogeneous spaces have been studied by a number of authors as a natural generalization of Riemannian symmetric spaces.0. Kowalski and L. Vanhecke drew their attention to the relationship between the naturally reductive spaces and the commutative spaces which are known to generalize symmetric spaces, as well. In this context they suppose that the Riemannian manifolds under consideration are connected, simply connected and complete.The three-dimensional naturally reductive spaces have been classified by F. Tricerri and L. Vanhecke [14]. 0. Kowalski found the same classification in a different context, and he also proved that the naturally reductive spaces and the commutative spaces form the same class in dimension three [9]. In the papers ([11], [12]) 0. Kowalski and L. Vanhecke gave the complete lassification for naturally reductive spaces as well as for the commutative spaces in dimension four. Once again, they proved that both classes coincide.In the paper [13] 0. Kowalski and L. Vanhecke gave the complete classification for the naturally reductive spaces in dimension five and they have also proved the commutativity of these spaces.The purpose of this paper is to prove the converse: all five-dimensional commutative spaces are naturally reductive.In this way we prove that, in dimensions three, four and five the class of naturally reductive spaces coincides with that of commutative spaces.In dimension 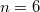 , the coincidente of naturally reductive spaces is not true any more.The six-dimensional generalized Heisenberg group with two-dimensional center is a commutative space, but it is not naturally reductive [5].On the other hand, the homogeneous space of the type
, the coincidente of naturally reductive spaces is not true any more.The six-dimensional generalized Heisenberg group with two-dimensional center is a commutative space, but it is not naturally reductive [5].On the other hand, the homogeneous space of the type 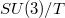 , where T is a maximal torus, being endowed with an arbitrary invariant Riemannian metric, is naturally reductive but not commutative [4].The paper is organized as follows: in the first section we give some necessary definitions and known facts conceming naturally reductive spaces and commutative spaces; in the second section, divided in some subsections, we shall prove the natural reductivity of five-dimensional spaces.
, where T is a maximal torus, being endowed with an arbitrary invariant Riemannian metric, is naturally reductive but not commutative [4].The paper is organized as follows: in the first section we give some necessary definitions and known facts conceming naturally reductive spaces and commutative spaces; in the second section, divided in some subsections, we shall prove the natural reductivity of five-dimensional spaces.
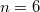 , the coincidente of naturally reductive spaces is not true any more.The six-dimensional generalized Heisenberg group with two-dimensional center is a commutative space, but it is not naturally reductive [5].On the other hand, the homogeneous space of the type
, the coincidente of naturally reductive spaces is not true any more.The six-dimensional generalized Heisenberg group with two-dimensional center is a commutative space, but it is not naturally reductive [5].On the other hand, the homogeneous space of the type 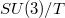 , where T is a maximal torus, being endowed with an arbitrary invariant Riemannian metric, is naturally reductive but not commutative [4].The paper is organized as follows: in the first section we give some necessary definitions and known facts conceming naturally reductive spaces and commutative spaces; in the second section, divided in some subsections, we shall prove the natural reductivity of five-dimensional spaces.
, where T is a maximal torus, being endowed with an arbitrary invariant Riemannian metric, is naturally reductive but not commutative [4].The paper is organized as follows: in the first section we give some necessary definitions and known facts conceming naturally reductive spaces and commutative spaces; in the second section, divided in some subsections, we shall prove the natural reductivity of five-dimensional spaces.DOI Code:
10.1285/i15900932v8n1p13
Full Text: PDF


