Metrizability of affine connections on analytic manifolds
Abstract
It is well-known (see e.g. [3]) that a torsion-free connection  on a connected smooth manifold M is a Riemannian connection of a Riemannian metric g if and only if its holonomy group
on a connected smooth manifold M is a Riemannian connection of a Riemannian metric g if and only if its holonomy group 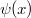 (with a fixed reference point
(with a fixed reference point 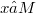 ) preserves a positive scalar product on the tangent space
) preserves a positive scalar product on the tangent space 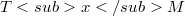 . In this paper we are occupied with the corresponding computational problems: a) How to decide effectively whether a given (torsion-free) connection is a Riemannian connection? b) In the positive case, how to find out effectively all corresponding Riemannian metrics (in the prescribed local coordinates) We shall solve both problems under the restriction that the basic manifold M is connected and simply connected, and that both M and the given connection
. In this paper we are occupied with the corresponding computational problems: a) How to decide effectively whether a given (torsion-free) connection is a Riemannian connection? b) In the positive case, how to find out effectively all corresponding Riemannian metrics (in the prescribed local coordinates) We shall solve both problems under the restriction that the basic manifold M is connected and simply connected, and that both M and the given connection  are analytic. Let us note that the problems above have been solved for very special cases in [l], [2], and in more general terms by the author in [4] and [5], where some kind of regularity for the curvature tensor was assumed. See also [6] and [7] for related results.
are analytic. Let us note that the problems above have been solved for very special cases in [l], [2], and in more general terms by the author in [4] and [5], where some kind of regularity for the curvature tensor was assumed. See also [6] and [7] for related results.
 on a connected smooth manifold M is a Riemannian connection of a Riemannian metric g if and only if its holonomy group
on a connected smooth manifold M is a Riemannian connection of a Riemannian metric g if and only if its holonomy group 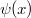 (with a fixed reference point
(with a fixed reference point 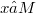 ) preserves a positive scalar product on the tangent space
) preserves a positive scalar product on the tangent space 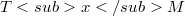 . In this paper we are occupied with the corresponding computational problems: a) How to decide effectively whether a given (torsion-free) connection is a Riemannian connection? b) In the positive case, how to find out effectively all corresponding Riemannian metrics (in the prescribed local coordinates) We shall solve both problems under the restriction that the basic manifold M is connected and simply connected, and that both M and the given connection
. In this paper we are occupied with the corresponding computational problems: a) How to decide effectively whether a given (torsion-free) connection is a Riemannian connection? b) In the positive case, how to find out effectively all corresponding Riemannian metrics (in the prescribed local coordinates) We shall solve both problems under the restriction that the basic manifold M is connected and simply connected, and that both M and the given connection  are analytic. Let us note that the problems above have been solved for very special cases in [l], [2], and in more general terms by the author in [4] and [5], where some kind of regularity for the curvature tensor was assumed. See also [6] and [7] for related results.
are analytic. Let us note that the problems above have been solved for very special cases in [l], [2], and in more general terms by the author in [4] and [5], where some kind of regularity for the curvature tensor was assumed. See also [6] and [7] for related results.DOI Code:
10.1285/i15900932v8n1p1
Full Text: PDF


