Two-norm spaces and summability
Abstract
We determine the general form of continuous linear functionals over the two-norm space of bounded Toeplitz summable sequences. From this we deduce some inclusion and consistency theorems. It was recognized many years ago [3], [7] that the two-normspace technique is the proper tool in investigation of the bounded efficiency field (ie.the set of bounded summable sequences) of Toeplitz methods. However these results were so far not presented in full extent in any paper, in particular the general form of γ-continuous functionals (for the definition see below) in those spaces was not given. We fill this gap, which enables us to obtain some inclusion theorems which lead in turn, to the well known consistency theorems of Mazur and Orlicz [6] in a sharpened form. We adopt the following notation and conventions. The terms of all sequences will be indexed starting with zero, the k-th element of the sequence x will be denoted by 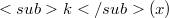 . The symbols
. The symbols 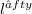 , c and
, c and 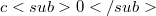 will stand for the space of bounded, convergent and to null convergent sequences, respectively;
will stand for the space of bounded, convergent and to null convergent sequences, respectively; 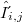 , will denote the Kronecker symbol.
, will denote the Kronecker symbol.
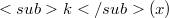 . The symbols
. The symbols 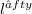 , c and
, c and 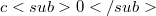 will stand for the space of bounded, convergent and to null convergent sequences, respectively;
will stand for the space of bounded, convergent and to null convergent sequences, respectively; 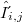 , will denote the Kronecker symbol.
, will denote the Kronecker symbol.DOI Code:
10.1285/i15900932v9n2p267
Full Text: PDF


