Flow-invariant sets
Abstract
Let S be a subset of some normed space E and let 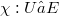 be a continuous function defined on an open subset U containing S. We consider functions
be a continuous function defined on an open subset U containing S. We consider functions ![x : [0,T] → U](http://siba-ese.unile.it/plugins/generic/latexRender/cache/aa8af7aa8dd176b5b120575a8bab7607.png) which satisfy the differential equation
which satisfy the differential equation 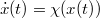 for all
for all ![t ∈ [0,T]](http://siba-ese.unile.it/plugins/generic/latexRender/cache/62a55d777f914c567cc814f9b2528fd0.png) , where T is a positive number, depending on z. Such functions will be called solutions of (1). We say that S is invarianC with reqhzt fo (l), if every solution of (1) with
, where T is a positive number, depending on z. Such functions will be called solutions of (1). We say that S is invarianC with reqhzt fo (l), if every solution of (1) with 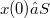 remainsin S,that is
remainsin S,that is ![([0,T]) ⊆ S](http://siba-ese.unile.it/plugins/generic/latexRender/cache/e1b25a065577f2d6d2f1023f51a2eef5.png) . Early results conceming the characterization of invariant sets in the finite dimensional case
. Early results conceming the characterization of invariant sets in the finite dimensional case 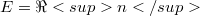 were obtained by Nagumo [Na42]. Further research was independently done by Bony [Bo69], Brezis [BGO], Crandall [Cr72], Hartman [Ha721 and Yorke Tyo673, [Yo70]. Different conditions imposed on S and x by Bony and Brezis respectively were related with one another by Redheffer [Re72]. He elucidated as well as generalized their results. There was even some progress in the case of infinite dimensional spaces. Redheffer and Walter [ReWa75] were the first to investigate this field. Their results were extended by Volkmann [Vo73], [Vo75]. Finally, Martin [Ma73] and Volkmann [Vo76] came to farreaching generalizations in case E is a Banach-space. This note offers an alternative approach based on an elementary lemma from the theory of functions of one real variable. As a corollary we obtain a slightly more general version of Brezis’ Invariance Theorem. In this fashion it becomes evident that the latter is a higher dimensional generalization of the lemma from one-dimensional calculus.
were obtained by Nagumo [Na42]. Further research was independently done by Bony [Bo69], Brezis [BGO], Crandall [Cr72], Hartman [Ha721 and Yorke Tyo673, [Yo70]. Different conditions imposed on S and x by Bony and Brezis respectively were related with one another by Redheffer [Re72]. He elucidated as well as generalized their results. There was even some progress in the case of infinite dimensional spaces. Redheffer and Walter [ReWa75] were the first to investigate this field. Their results were extended by Volkmann [Vo73], [Vo75]. Finally, Martin [Ma73] and Volkmann [Vo76] came to farreaching generalizations in case E is a Banach-space. This note offers an alternative approach based on an elementary lemma from the theory of functions of one real variable. As a corollary we obtain a slightly more general version of Brezis’ Invariance Theorem. In this fashion it becomes evident that the latter is a higher dimensional generalization of the lemma from one-dimensional calculus.
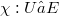 be a continuous function defined on an open subset U containing S. We consider functions
be a continuous function defined on an open subset U containing S. We consider functions ![x : [0,T] → U](http://siba-ese.unile.it/plugins/generic/latexRender/cache/aa8af7aa8dd176b5b120575a8bab7607.png) which satisfy the differential equation
which satisfy the differential equation 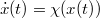 for all
for all ![t ∈ [0,T]](http://siba-ese.unile.it/plugins/generic/latexRender/cache/62a55d777f914c567cc814f9b2528fd0.png) , where T is a positive number, depending on z. Such functions will be called solutions of (1). We say that S is invarianC with reqhzt fo (l), if every solution of (1) with
, where T is a positive number, depending on z. Such functions will be called solutions of (1). We say that S is invarianC with reqhzt fo (l), if every solution of (1) with 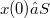 remainsin S,that is
remainsin S,that is ![([0,T]) ⊆ S](http://siba-ese.unile.it/plugins/generic/latexRender/cache/e1b25a065577f2d6d2f1023f51a2eef5.png) . Early results conceming the characterization of invariant sets in the finite dimensional case
. Early results conceming the characterization of invariant sets in the finite dimensional case 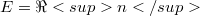 were obtained by Nagumo [Na42]. Further research was independently done by Bony [Bo69], Brezis [BGO], Crandall [Cr72], Hartman [Ha721 and Yorke Tyo673, [Yo70]. Different conditions imposed on S and x by Bony and Brezis respectively were related with one another by Redheffer [Re72]. He elucidated as well as generalized their results. There was even some progress in the case of infinite dimensional spaces. Redheffer and Walter [ReWa75] were the first to investigate this field. Their results were extended by Volkmann [Vo73], [Vo75]. Finally, Martin [Ma73] and Volkmann [Vo76] came to farreaching generalizations in case E is a Banach-space. This note offers an alternative approach based on an elementary lemma from the theory of functions of one real variable. As a corollary we obtain a slightly more general version of Brezis’ Invariance Theorem. In this fashion it becomes evident that the latter is a higher dimensional generalization of the lemma from one-dimensional calculus.
were obtained by Nagumo [Na42]. Further research was independently done by Bony [Bo69], Brezis [BGO], Crandall [Cr72], Hartman [Ha721 and Yorke Tyo673, [Yo70]. Different conditions imposed on S and x by Bony and Brezis respectively were related with one another by Redheffer [Re72]. He elucidated as well as generalized their results. There was even some progress in the case of infinite dimensional spaces. Redheffer and Walter [ReWa75] were the first to investigate this field. Their results were extended by Volkmann [Vo73], [Vo75]. Finally, Martin [Ma73] and Volkmann [Vo76] came to farreaching generalizations in case E is a Banach-space. This note offers an alternative approach based on an elementary lemma from the theory of functions of one real variable. As a corollary we obtain a slightly more general version of Brezis’ Invariance Theorem. In this fashion it becomes evident that the latter is a higher dimensional generalization of the lemma from one-dimensional calculus.DOI Code:
10.1285/i15900932v9n2p221
Full Text: PDF


